Clifford theorem

A theorem establishing an inequality between the degree and the dimension of a special divisor on an algebraic curve. It was proved by W. Clifford.

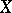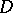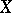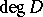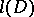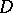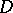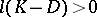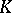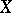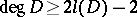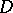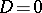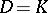Let be a smooth projective curve over an algebraically closed field, and let be a divisor on . Let be the degree and the dimension of . A positive divisor is called special if , where is the canonical divisor on . Clifford's theorem states: for any special divisor , with equality if or or if 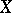is a hyper-elliptic curve and 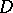is a multiple of the unique special divisor of degree 2 on 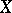. An equivalent statement of Clifford's theorem is: 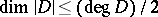, where 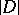is the linear system of 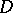. It follows from Clifford's theorem that the above inequality holds for any divisor 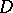on 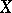for which 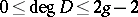, where 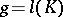is the genus of .

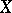References

[1]	R.J. Walker, "Algebraic curves" , Springer (1978)
[2]	N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian)
[3]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[4]	R. Hartshorne, "Algebraic geometry" , Springer (1977)

References

[a1]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978)
[a2]	E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985)