Abstract analytic function

analytic mapping of Banach spaces

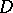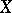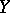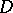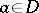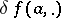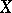A function acting from some domain of a Banach space into a Banach space that is differentiable according to Fréchet everywhere in , i.e. is such that for any point there exists a bounded linear operator from into 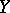for which the following relation is true:

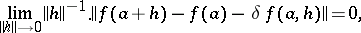where 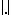denotes the norm on or on 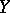; 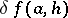is called the Fréchet differential of 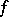at .

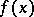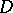Another approach to the notion of an abstract analytic function is based on differentiability according to Gâteaux. A function from into 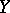is weakly analytic in 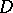, or differentiable according to Gâteaux in 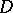, if for each continuous linear functional 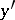on 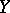and each element 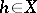the complex function 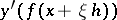is a holomorphic function of the complex variable 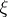in the disc 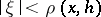, where . Any abstract analytic function in a domain 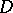is continuous and weakly analytic in 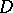. The converse proposition is also true, and the continuity condition can be replaced by local boundedness or by continuity according to Baire.

The term "abstract analytic function" is sometimes employed in a narrower sense, when it means a function 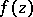of a complex variable with values in a Banach space or even in a locally convex linear topological space 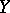. In such a case any weakly analytic function 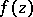in a domain 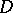of the complex plane 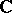is an abstract analytic function. One can also say that a function 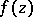is an abstract analytic function in a domain 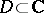if and only if 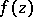is continuous in 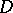and if for any simple closed rectifiable contour 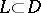the integral vanishes. For an abstract analytic function 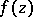of a complex variable the Cauchy formula (cf. Cauchy integral) is valid.

Let 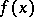be a weakly analytic function in a domain 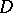of a Banach space . Then 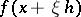, as a function of the complex variable 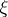, has derivatives of all orders in the domain 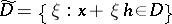, , 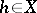these derivatives being abstract analytic functions from 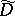into 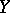. If the set 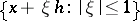belongs to 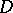, then

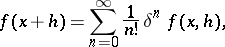where the series converges in norm, and

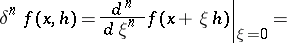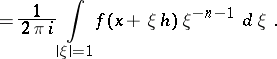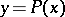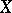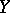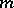A function from into is called a polynomial with respect to the variable of degree at most if, for all 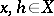and for all complex 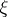, one has

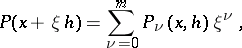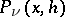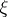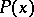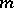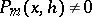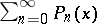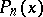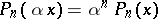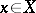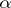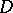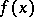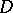where the functions are independent of . The degree of is exactly if . A power series is a series of the form where are homogeneous polynomials of degree so that , , for all complex . An arbitrary weakly convergent power series in a domain converges in norm towards some weakly analytic function in , and 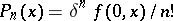, 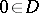. A function 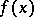is an abstract analytic function if and only if it can be developed in a power series in a neighbourhood of all points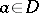

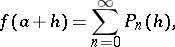where all 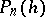are continuous in .

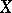Many fundamental results in the classical theory of analytic functions — such as the maximum-modulus principle, the uniqueness theorems, the Vitali theorem, the Liouville theorem, etc. — are applicable to abstract analytic functions if suitable changes are introduced. The set of all analytic functions in a domain 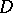forms a linear space.

The notion of an abstract analytic function can be generalized to wider classes of spaces 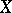and 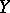, such as locally convex topological spaces, Banach spaces over an arbitrary complete valuation field, etc.

References

[1]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)
[2]	R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)
[3]	L. Schwartz, "Cours d'analyse" , 2 , Hermann (1967)