Euler-Frobenius polynomials

The Euler–Frobenius polynomials of degree are characterized by the Frobenius reciprocal identity ([a1], [a2], [a3])

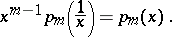Thus, is invariant under the reflection

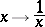of the indeterminate . The best way to implement an invariance of this kind is to look for an appropriate space with which the Euler–Frobenius polynomials 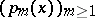are attached in a spectral geometric way.

So, let denote a symplectic vector space of dimension (cf. also Symplectic space). Then the characteristic polynomial of each symplectic automorphism of 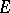is an Euler–Frobenius polynomial 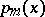of odd degree .

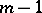The proof follows from the fact that the determinant of each symplectic automorphism of 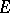equals , so that there is a natural imbedding

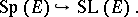Thus, 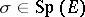preserves the symplectic volume spanned by 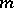vectors of the vector space .

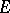A consequence is that each eigenvalue 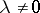of a symplectic endomorphism 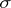of having multiplicity gives rise to a reciprocal eigenvalue 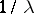of the same multiplicity .

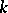In view of the self-reciprocal eigenvalue

of 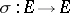for even , of course, spectral theory suggests a complex contour integral representation of the Euler–Frobenius polynomials 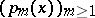, as follows.

Let 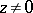denote a complex number such tha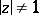t . Let 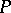denote a path in the complex plane 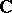which forms the boundary of a closed vertical strip in the open right or left half-plane of 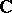according as 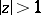or 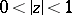, respectively. Let 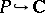be oriented so that its topological index satisfies 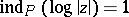. Then, for each integer 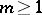, the complex contour integral representation

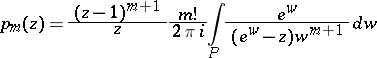holds.

The proof follows from the expansion

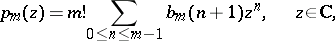with strictly positive integer coefficients, where 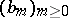denote the basis spline functions (cf. [a3] and also Spline).

A consequence is that the Euler–Frobenius polynomials provide the coefficients of the local power series expansion of the function

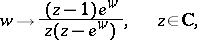which is meromorphic on the complex plane .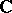

The Euler–Frobenius polynomials 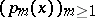satisfy the three-term recurrence relation

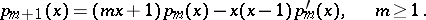A direct proof follows from the complex contour integral representations of the derivatives , which can be derived from the complex contour integral representation given above for the Euler–Frobenius polynomials.

The preceding recurrence relation opens a simple way to calculate the coefficients of the Euler–Frobenius polynomials 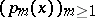([a1], [a3]).

References

[a1]	L. Euler, "Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum" , Acad. Imper. Sci. Petropolitanæ (1775) (Opera Omnis Ser. I (Opera Math.), Vol. X, Teubner, 1913)
[a2]	F.G. Frobenius, "Über die Bernoullischen Zahlen und die Eulerschen Polynome" Sitzungsber. K. Preuss. Akad. Wissenschaft. Berlin (1910) pp. 809–847 (Gesammelte Abh. Vol. III, pp. 440-478, Springer 1968)
[a3]	W. Schempp, "Complex contour integral representation of cardinal spline functions" , Contemp. Math. , 7 , Amer. Math. Soc. (1982)