Exhaustion of a domain

approximating sequence of domains

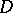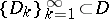For a given domain in a topological space , an exhaustion is a sequence of (in a certain sense regular) domains such that and 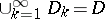. For any domain 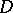in a complex space 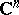there exists an exhaustion by domains 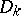that are, e.g., bounded by piecewise-smooth curves (in 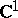) or by piecewise-smooth surfaces (in 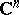, 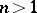). For any Riemann surface 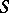there is a polyhedral exhaustion , consisting of polyhedral domains 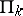that are, each individually, connected unions of a finite number of triangles in a triangulation of ; moreover, 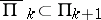, , and the boundary of each of the domains making up the open set is, for sufficiently large 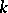, just one of the boundary contours of .

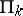References

[1]	S. Stoilov, "The theory of functions of a complex variable" , 2 , Moscow (1962) pp. Chapt. 5 (In Russian; translated from Rumanian)

Comments

The fact that any pseudo-convex domain (cf. Pseudo-convex and pseudo-concave) can be exhausted by smooth, strictly pseudo-convex domains is of fundamental importance in higher-dimensional complex analysis, cf. [a2].

References

[a1]	G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10
[a2]	L.V. Ahlfors, L. Sario, "Riemann surfaces" , Princeton Univ. Press (1960) pp. Chapt. 1
[a3]	S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Sect. 7.1