Winding number
Let 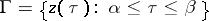 be an arc in the complex plane and let
be an arc in the complex plane and let  be a point not on
be a point not on 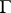 . A continuous argument of
. A continuous argument of 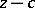 on
on 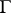 is a continuous real-valued function
is a continuous real-valued function 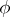 on
on  that for each
that for each 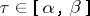 is an argument of
is an argument of 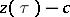 , i.e.
, i.e. 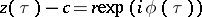 for some
for some  . Such functions can be found, and if
. Such functions can be found, and if  ,
, 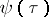 are two continuous arguments, then they differ by a constant integral multiple of
are two continuous arguments, then they differ by a constant integral multiple of 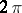 . It follows that the increase of the argument,
. It follows that the increase of the argument, 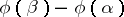 , does not depend on the choice of the continuous argument. It is denoted by
, does not depend on the choice of the continuous argument. It is denoted by 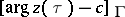 . If
. If 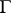 is a piecewise-regular arc,
is a piecewise-regular arc,
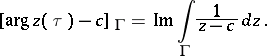 |
In the special case that 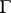 is a closed curve, i.e.
is a closed curve, i.e. 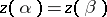 ,
,  is necessarily an integral multiple of
is necessarily an integral multiple of 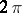 and the integer
and the integer
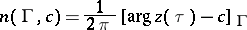 |
is called the winding number of 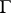 with respect to
with respect to  . For a piecewise-regular closed curve
. For a piecewise-regular closed curve 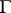 with
with  not on
not on 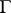 one has
one has
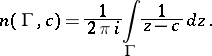 |
References
| [a1] | P. Henrici, "Applied and computational complex analysis" , 1 , Wiley (Interscience) (1974) pp. §4.6 |
Winding number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Winding_number&oldid=17188