Bitsadze equation
The partial differential equation that can be written in complex form as follows:
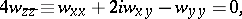 |
where  , and that can be reduced to the elliptic system
, and that can be reduced to the elliptic system
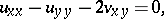 |
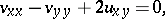 |
in the real independent variables  and
and 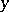 . The homogeneous Dirichlet problem in a disc
. The homogeneous Dirichlet problem in a disc  :
:  , where the radius
, where the radius  is as small as one pleases, for the Bitsadze equation has an infinite number of linearly independent solutions [1]. The Dirichlet problem for the inhomogeneous equation
is as small as one pleases, for the Bitsadze equation has an infinite number of linearly independent solutions [1]. The Dirichlet problem for the inhomogeneous equation 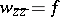 in the disc
in the disc 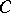 is normally solvable according to Hausdorff, since it is neither a Fredholm problem nor Noetherian; in a bounded domain containing a segment of the straight line
is normally solvable according to Hausdorff, since it is neither a Fredholm problem nor Noetherian; in a bounded domain containing a segment of the straight line 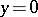 , this problem is not even a Hausdorff problem, even though the homogeneous problem has only one zero solution [2].
, this problem is not even a Hausdorff problem, even though the homogeneous problem has only one zero solution [2].
References
| [1] | A.V. Bitsadze, "On the uniqueness of the solution of the Dirichlet problem for elliptic partial differential operators" Uspekhi Mat. Nauk , 3 : 6 (1948) pp. 211–212 (In Russian) |
| [2] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
| [3] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [4] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
Bitsadze equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bitsadze_equation&oldid=17152