Locally nilpotent group

A group in which every finitely-generated subgroup is nilpotent (see Nilpotent group; Finitely-generated group). In a locally nilpotent group the elements of finite order form a normal subgroup, the torsion part of this group (cf. Periodic group). This subgroup is the direct product of its Sylow subgroups, and the quotient group with respect to it is torsion-free. A locally nilpotent torsion-free group (cf. Group without torsion) has the uniqueness-of-roots property: If, for elements and and 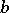any integer 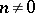, one has 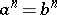, then 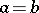. Every locally nilpotent torsion-free group 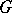has a Mal'tsev completion, that is, it can be imbedded in a unique locally nilpotent torsion-free group 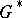such that all equations of the form 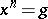are solvable in 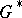, where 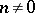and 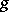is any element of 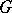. This completion is functorial, that is, any homomorphism 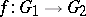of locally nilpotent torsion-free groups 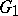and 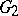can be uniquely extended to a homomorphism .

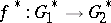References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)
[2]	M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian)