Keldysh-Lavrent'ev theorem

on uniform approximation by entire functions

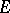In order that there exist for any continuous complex-valued function on a continuum and any rapidly-decreasing positive function , (as ), having a positive lower bound on any finite interval, an entire function such that

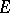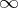it is necessary and sufficient that has no interior points and that there exists a function , , that increases to and is such that any point of the complement can be joined to by a Jordan curve situated outside and outside the disc .

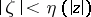This result of M.V. Keldysh and M.A. Lavrent'ev [1] summarizes numerous investigations on approximation by entire functions initiated by the Carleman theorem (Section 3; see also [2]).

References

[1]	M.V. Keldysh, M.A. Lavrent'ev, "Sur un problème de M. Carleman" Dokl. Akad. Nauk SSSR , 23 : 8 (1939) pp. 746–748
[2]	S.N. Mergelyan, "Uniform approximation to functions of a complex variable" Transl. Amer. Math. Soc. , 3 (1962) pp. 294–391 Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 31–1A2

References

[a1]	D. Gaier, "Lectures on complex approximation" , Birkhäuser (1987) (Translated from German)