Repelling set

repellor, in a dynamical system .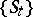

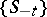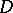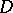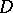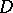A subset of the phase space of the system that is an attractor for the reverse system . In general, an attractor of a dynamical system (cf. also Routes to chaos) is a non-empty subset of the phase space such that all trajectories from a neighbourhood of tend to when time increases. More precisely, let be the domain of attraction (or basin) of , i.e. the set of all points 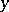in the phase space for which 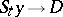as 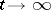(that is, for every neighbourhood 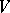of 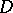there is an 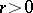such that 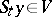for all 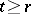). 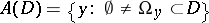If the phase space is locally compact and is compact, then , where 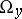is the 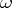-limit set of 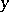(cf. Limit set of a trajectory) (certain authors take this as a definition of 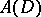in the general case). Now, a subset 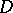of the phase space is called an attractor whenever 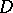has an open neighbourhood 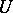such that 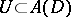; in that case 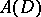is an open invariant subset of the phase space. If an attractor, respectively repellor, consists of one point, then one speaks of an attracting, respectively repelling, point. For details (e.g., on stability of attractors) see [a1]. It should be noted that in other literature the definition of an attractor is what is called a stable attractor in [a1]. For discussions on the "correct" definition of an attractor see [a2], Sect. 5.4, and [a3]. See also Strange attractor.

References

[a1]	N.P. Bahtia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970)
[a2]	J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983)
[a3]	D. Ruelle, "Small random perturbations of dynamical systems and the definition of attractors" Comm. Math. Phys. , 82 (1981) pp. 137–151