Annihilator
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
left, of a set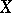 
in 
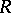
The set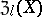 
of all elements 
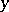in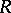 
such that 
. Here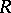 
is a ring or a semi-group (or, generally, a groupoid) with a zero. The right annihilator of a set 
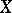in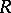 
is defined in a similar manner as the set
 |
The set
 |
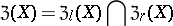is the two-sided annihilator of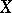 
. In an associative ring (or semi-group) 
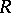the left annihilator of an arbitrary set 
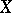is a left ideal, and if 
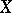is a left ideal of 
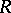, then 
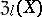is a two-sided ideal of 
; in the non-associative case these statements are usually not true.
How to Cite This Entry:
Annihilator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Annihilator&oldid=17045
Annihilator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Annihilator&oldid=17045
This article was adapted from an original article by K.A. Zhevlakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article