Reductio ad absurdum

A logical derivation rule that allows one to conclude that if a list of statements and a statement 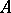imply both a statement 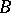and the statement , then implies 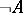. The rule of reductio ad absurdum can, e.g., be written in the form

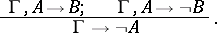Reductio ad absurdum is a sound rule in the majority of logico-mathematical calculi.

Comments

Informally, the name "reductio ad absurdum" is also used for the rule that if together with implies a contradiction, then implies . This is of course equivalent to the above (and therefore sound) in classical logic, but it is not a sound rule of inference in intuitionistic logic.