Principal fibre bundle

A -fibration such that the group acts freely and perfectly on the space . The significance of principal fibre bundles lies in the fact that they make it possible to construct associated fibre bundles with fibre if a representation of 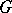in the group of homeomorphisms is given. Differentiable principal fibre bundles with Lie groups play an important role in the theory of connections and holonomy groups. For instance, let be a topological group with as a closed subgroup and let 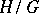be the homogeneous space of left cosets of 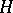with respect to 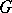; the fibre bundle 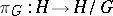will then be principal. Further, let 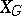be a Milnor construction, i.e. the join of an infinite number of copies of , each point of which has the form

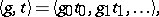where 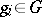, , 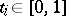and where only finitely many 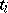are non-zero. The action of 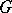on 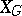defined by the formula 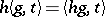is free, and the fibre bundle 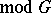is a numerable principal fibre bundle.

Each fibre of a principal fibre bundle is homeomorphic to .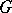

A morphism of principal fibre bundles is a morphism of the fibre bundles 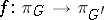for which the mapping of the fibres 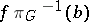induces a homomorphism of groups:

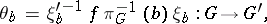where 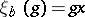, 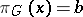. In particular, a morphism is called equivariant if 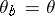is independent of 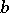, so that 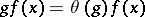for any 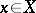, 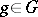. If and , an equivariant morphism is called a 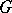-morphism. Any 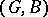-morphism (i.e. a 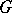-morphism over 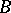) is called a 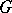-isomorphism.

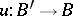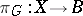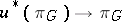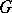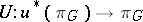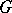For any mapping and principal fibre bundle the induced fibre bundle is principal with the same group ; moreover, the mapping is a -morphism which unambiguously determines the action of 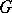on the space 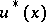. For instance, if the principal fibre bundle 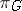is trivial, it is isomorphic to the principal fibre bundle 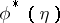, where 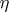is the 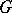-bundle over a single point and 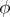is the constant mapping. The converse is also true, and for this reason principal fibre bundles with a section are trivial. For each numerable principal fibre bundle 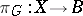there exists a mapping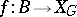 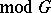such that 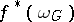is -is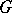omorphic to 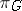, and for the principal fibre bundles and 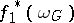to be isomorphic, it is necessary and sufficient that 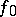and 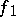be homotopic (cf. Homotopy). This is the principal theorem on the homotopy classification of principal fibre bundles, which expresses the universality of the principal fibre bundle 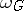(obtained by Milnor's construction), with respect to the classifying mapping .

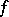References

[1]	R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964)
[2]	K. Nomizu, "Lie groups and differential geometry" , Math. Soc. Japan (1956)
[3]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964)
[4]	, Fibre spaces and their applications , Moscow (1958) (In Russian; translated from English)
[5]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)
[6]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)

Comments

Let be a principal fibre bundle. It is called numerable if there is a sequence 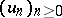of continuous mappings 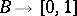such that the open sets 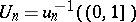form an open covering (cf. Covering (of a set)) of 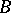and 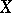is trivializable over each 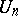(i.e. the restricted bundles 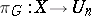are trivial, cf. Fibre space).

References

[a1]	J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989)