Glueing theorems
Theorems that establish the existence of analytic functions subject to prescribed relations on the boundary of a domain.
Lavrent'ev's glueing theorem [1]: Given any analytic function 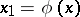 on
on 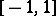 with
with 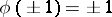 and
and  , then one can construct two analytic functions
, then one can construct two analytic functions 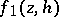 and
and 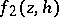 , where
, where 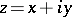 and
and 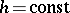 , mapping the rectangles
, mapping the rectangles 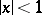 ,
, 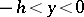 and
and 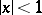 ,
, 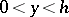 univalently and conformally onto disjoint domains
univalently and conformally onto disjoint domains 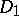 and
and 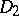 , respectively, in such a way that
, respectively, in such a way that 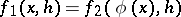 . This theorem was used (see [6]) to prove the existence of a function
. This theorem was used (see [6]) to prove the existence of a function 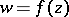 ,
, 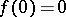 ,
, 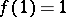 , realizing a quasi-conformal mapping of the disc
, realizing a quasi-conformal mapping of the disc 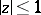 onto the disc
onto the disc  and possessing almost-everywhere a given characteristic
and possessing almost-everywhere a given characteristic 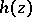 , where
, where
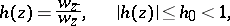 |
and 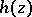 is a measurable function defined for almost-all
is a measurable function defined for almost-all 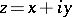 ,
, 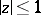 . A modified form of Lavrent'ev's theorem was also used to solve the problem of mapping a simply-connected Riemann surface conformally onto the disc [5].
. A modified form of Lavrent'ev's theorem was also used to solve the problem of mapping a simply-connected Riemann surface conformally onto the disc [5].
Other glueing theorems (with weaker restrictions on the functions of type 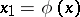 , see [2]) have played a major role in the theory of Riemann surfaces. Another example is as follows (see [3], [5]): Suppose one is given an arc
, see [2]) have played a major role in the theory of Riemann surfaces. Another example is as follows (see [3], [5]): Suppose one is given an arc 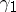 on the circle
on the circle  with end points
with end points  and
and 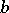 ,
, 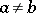 , and a function
, and a function  on
on 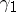 with the properties: 1) at all the interior points of
with the properties: 1) at all the interior points of 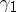 ,
,  is regular and
is regular and 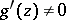 ; 2) the function
; 2) the function 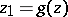 establishes a one-to-one mapping of
establishes a one-to-one mapping of 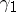 onto the complementary arc
onto the complementary arc 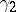 on
on  leaving
leaving  and
and  invariant. Then there is a function
invariant. Then there is a function
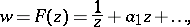 |
regular for 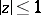 except at
except at 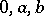 , such that
, such that  at the interior points of
at the interior points of 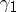 .
.
It has also been proved that there is a univalent function 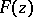 with these properties (see [4], Chapt. 2).
with these properties (see [4], Chapt. 2).
References
| [1] | M.A. Lavrent'ev, "Sur une classe de répresentations continues" Mat. Sb. , 42 : 4 (1935) pp. 407–424 |
| [2] | L.I. Volkovyskii, "On the problem of the connectedness type of Riemann surfaces" Mat. Sb. , 18 : 2 (1946) pp. 185–212 (In Russian) |
| [3] | A.C. Schaeffer, D.C. Spencer, "Variational methods in conformal mapping" Duke Math. J. , 14 : 4 (1947) pp. 949–966 |
| [4] | A.C. Schaeffer, D.C. Spencer, "Coefficient regions for schlicht functions" , Amer. Math. Soc. Coll. Publ. , 35 , Amer. Math. Soc. (1950) |
| [5] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [6] | P.P. Belinskii, "General properties of quasi-conformal mappings" , Novosibirsk (1974) pp. Chapt. 2, Par. 1 (In Russian) |
Glueing theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Glueing_theorems&oldid=16815