Cosine amplitude
From Encyclopedia of Mathematics
elliptic cosine
One of the three basic Jacobi elliptic functions, denoted by
 |
The cosine amplitude is expressible in terms of the Weierstrass sigma-functions, the Jacobi theta-functions or a power series, as follows:
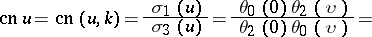 |
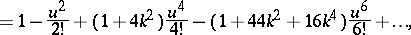 |
where  is the modulus of the elliptic function,
is the modulus of the elliptic function, 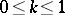 ;
; 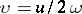 , and
, and  . For
. For 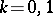 one has, respectively,
one has, respectively, 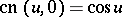 ,
, 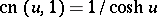 .
.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 2 , Springer (1964) pp. Chapt. 3 |
Comments
More on the function 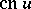 , e.g. derivatives, evenness, behaviour on the real line, etc. can be found in [a1].
, e.g. derivatives, evenness, behaviour on the real line, etc. can be found in [a1].
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) (Translated from Russian) |
How to Cite This Entry:
Cosine amplitude. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cosine_amplitude&oldid=16678
Cosine amplitude. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cosine_amplitude&oldid=16678
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article