Domain invariance
Let 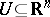 be open. If
be open. If 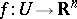 is a one-to-one continuous function, then
is a one-to-one continuous function, then 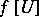 is open and
is open and 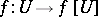 is a homeomorphism. This is called the Brouwer invariance of domain theorem, and was proved by L.E.J. Brouwer in [a1]. This result immediately implies that if
is a homeomorphism. This is called the Brouwer invariance of domain theorem, and was proved by L.E.J. Brouwer in [a1]. This result immediately implies that if 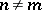 , then
, then  and
and 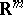 are not homeomorphic. A similar result for infinite-dimensional vector spaces does not hold, as the subspace
are not homeomorphic. A similar result for infinite-dimensional vector spaces does not hold, as the subspace 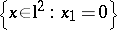 of
of 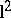 shows. But Brouwer's theorem can be extended to compact fields in Banach spaces of type
shows. But Brouwer's theorem can be extended to compact fields in Banach spaces of type 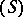 , as was shown by J. Schauder [a3]. Here, a compact field (a name coming from "compact vector field" ) is a mapping of the form
, as was shown by J. Schauder [a3]. Here, a compact field (a name coming from "compact vector field" ) is a mapping of the form 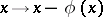 , with
, with 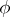 a compact mapping. A more general result for arbitrary Banach spaces was established (by using degree theory for compact fields) by J. Leray [a2]. Several important results in the theory of differential equations were proved by using domain invariance as a tool.
a compact mapping. A more general result for arbitrary Banach spaces was established (by using degree theory for compact fields) by J. Leray [a2]. Several important results in the theory of differential equations were proved by using domain invariance as a tool.
References
| [a1] | L.E.J. Brouwer, "Invariantz des  -dimensionalen Gebiets" Math. Ann. , 71/2 (1912/3) pp. 305–313; 55–56 -dimensionalen Gebiets" Math. Ann. , 71/2 (1912/3) pp. 305–313; 55–56 |
| [a2] | J. Leray, "Topologie des espaces abstraits de M. Banach" C.R. Acad. Sci. Paris , 200 (1935) pp. 1083–1093 |
| [a3] | J. Schauder, "Invarianz des Gebietes in Funktionalräumen" Studia Math. , 1 (1929) pp. 123–139 |
Domain invariance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domain_invariance&oldid=16623