Conductor of an Abelian extension
Let 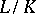 be an Abelian extension and let
be an Abelian extension and let 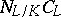 be the corresponding subgroup of the idèle class group
be the corresponding subgroup of the idèle class group 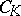 (cf. Class field theory). The conductor of an Abelian extension is the greatest common divisor of all positive divisors
(cf. Class field theory). The conductor of an Abelian extension is the greatest common divisor of all positive divisors  such that
such that 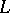 is contained in the ray class field
is contained in the ray class field 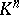 .
.
For an Abelian extension of local fields 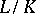 the conductor of
the conductor of 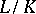 is
is 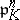 , where
, where 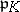 is the maximal ideal of (the ring of integers
is the maximal ideal of (the ring of integers 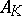 of)
of) 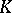 and
and  is the smallest integer such that
is the smallest integer such that 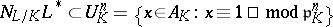 ,
, 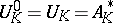 . (Thus, an Abelian extension is unramified if and only if its conductor is
. (Thus, an Abelian extension is unramified if and only if its conductor is 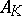 .) The link between the local and global notion of a conductor of an Abelian extension is given by the theorem that the conductor
.) The link between the local and global notion of a conductor of an Abelian extension is given by the theorem that the conductor 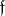 of an Abelian extension
of an Abelian extension 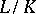 of number fields is equal to
of number fields is equal to 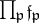 , where
, where 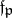 is the conductor of the corresponding local extension
is the conductor of the corresponding local extension 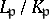 . Here for the infinite primes,
. Here for the infinite primes, 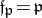 or
or 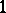 according to whether
according to whether 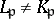 or
or 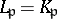 .
.
The conductor ramification theorem of class field theory says that if 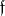 is the conductor of a class field
is the conductor of a class field 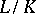 , then
, then 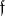 is not divisible by any prime divisor which is unramified for
is not divisible by any prime divisor which is unramified for 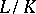 and
and 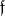 is divisible by any prime divisor that does ramify for
is divisible by any prime divisor that does ramify for 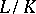 .
.
If 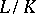 is the cyclic extension of a local field
is the cyclic extension of a local field 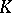 with finite or algebraically closed residue field defined by a character
with finite or algebraically closed residue field defined by a character 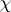 of degree 1 of
of degree 1 of 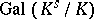 , then the conductor of
, then the conductor of 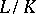 is equal to
is equal to 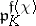 , where
, where 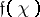 is the Artin conductor of the character
is the Artin conductor of the character  (cf. Conductor of a character). Here
(cf. Conductor of a character). Here 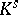 is the separable algebraic closure of
is the separable algebraic closure of 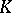 . There is no such interpretation known for characters of higher degree.
. There is no such interpretation known for characters of higher degree.
References
| [a1] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) |
| [a2] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. 4, Sect. 8 |
Conductor of an Abelian extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conductor_of_an_Abelian_extension&oldid=16618