Semi-Markov process
A stochastic process 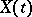 with a finite or countable set of states
with a finite or countable set of states  , having stepwise trajectories with jumps at times
, having stepwise trajectories with jumps at times  and such that the values
and such that the values  at its jump times form a Markov chain with transition probabilities
at its jump times form a Markov chain with transition probabilities
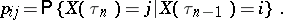 |
The distributions of the jump times 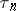 are described in terms of the distribution functions
are described in terms of the distribution functions 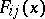 as follows:
as follows:
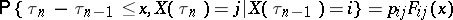 |
(and, moreover, they are independent of the states of the process at earlier moments of time). If
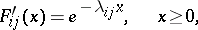 |
for all 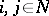 , then the semi-Markov process
, then the semi-Markov process 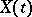 is a continuous-time Markov chain. If all the distributions degenerate to a point, the result is a discrete-time Markov chain.
is a continuous-time Markov chain. If all the distributions degenerate to a point, the result is a discrete-time Markov chain.
Semi-Markov processes provide a model for many processes in queueing theory and reliability theory. Related to semi-Markov processes are Markov renewal processes (see Renewal theory), which describe the number of times the process 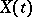 is in state
is in state 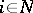 during the time
during the time 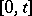 .
.
In analytic terms, the investigation of semi-Markov processes and Markov renewal processes reduces to a system of integral equations — the renewal equations.
References
| [1] | V.S. Korolyuk, A.F. Turbin, "Semi-Markov processes and their applications" , Kiev (1976) (In Russian) |
Comments
References
| [a1] | E. Cinlar, "Introduction to stochastic processes" , Prentice-Hall (1975) pp. Chapt. 10 |
Semi-Markov process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-Markov_process&oldid=16357