Diophantine predicate

Any predicate 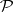defined on the set of (ordered) -tuples of integers (or non-negative integers or positive integers) for which there exists a polynomial 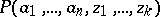with integer coefficients such that the -tuple 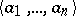satisfies the predicate 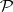if and only if the Diophantine equation (cf. Diophantine equations)

(*)

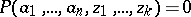is solvable with respect to . The truth domain of a Diophantine predicate is a Diophantine set. The class of Diophantine predicates coincides with the class of recursively enumerable predicates (cf. Diophantine equations, solvability problem of).

Comments

The truth domain of a Diophantine predicate 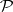is the set of all -tuples 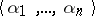satisfying 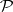, i.e., for which (*) is solvable with respect to .