Vector ring
From Encyclopedia of Mathematics
A partially ordered ring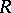 
(cf. Partially ordered set) which is a subdirect sum of totally ordered rings 
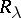(cf. Totally ordered set). Each element of a vector ring is a vector
 |
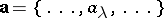with coordinates in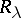 
, and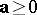 
if and only if each 
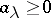. If the partial order of 
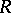is an intersection of total orders, 
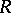will be a vector ring, and 
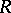itself, provided with various linear extensions of its partial order, may be taken as 
.
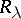References
| [1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
How to Cite This Entry:
Vector ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_ring&oldid=16239
Vector ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_ring&oldid=16239
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article