Riesz product

An infinite product of the form

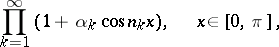(1)

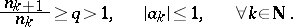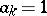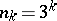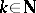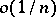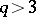With the help of such products (, for all ) F. Riesz indicated the first example of a continuous function of bounded variation whose Fourier coefficients are not of order . If , then the identity

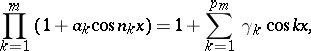gives the series

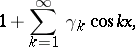(2)

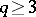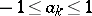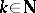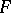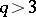which is said to represent the Riesz product (1). In case , for all , the series (2) is the Fourier–Stieltjes series of a non-decreasing continuous function . If and

then 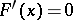almost-everywhere. If, in addition, 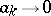, then the series (2) converges to zero almost-everywhere.

A number of problems, mainly in the theory of trigonometric series, has been solved using a natural generalization of the Riesz product when in (1) 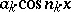is replaced by specially chosen trigonometric polynomials .

References

[1]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[2]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)