Conjugate net

A net of lines on a surface consisting of two families of lines such that at every point of the surface the lines from the two families of the net have conjugate directions. If a coordinate net is a conjugate net, then the coefficient 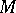of the second fundamental form of the surface is identically equal to zero. In a neighbourhood of every point of the surface which is not a flat point one can introduce a parametrization such that the coordinate lines form a conjugate net. One family can be chosen arbitrarily, even when the lines of this family do not have asymptotic directions. An important example is a net of lines of curvature.

References

[1]	A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian)

References

[a1]	C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4