Anger function
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The function
 | (*) |
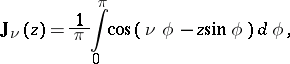which satisfies the inhomogeneous Bessel equation:
 |
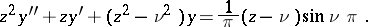For integers 
is the Bessel function of order 
(cf. Bessel functions). For non-integer 
the following expansion is valid:
 |
 |
 |
 |
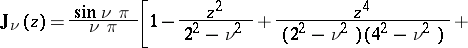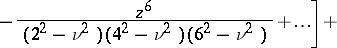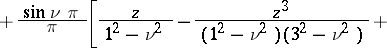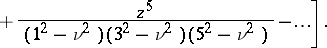The asymptotic expansion
 |
 |
 |
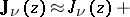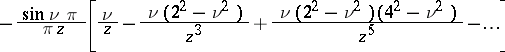is valid for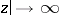 
and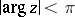 
.
The functions have been named after C.T. Anger [1], who studied functions of the type (*), but with 
as the upper limit of the integral.
References
| [1] | C.T. Anger, Neueste Schr. d. Naturf. d. Ges. i. Danzig , 5 (1855) pp. 1–29 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952) |
How to Cite This Entry:
Anger function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anger_function&oldid=16115
Anger function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anger_function&oldid=16115
This article was adapted from an original article by A.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article