Modulus of an annulus
The value reciprocal to the extremal length of the family of closed curves in the annulus  which separate the boundary circles; the modulus is equal to
which separate the boundary circles; the modulus is equal to
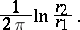 |
By a conformal mapping onto an associated annulus  , the modulus
, the modulus  of an annular domain
of an annular domain  can be obtained. It turns out that
can be obtained. It turns out that  , where
, where  is the Dirichlet integral of the real part of the function
is the Dirichlet integral of the real part of the function  mapping
mapping  onto
onto 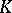 :
: 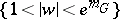 . (Thus, a given annular domain is mapped onto an annulus with a fixed ratio of the radii of the boundary circles. This fact can be taken as another definition of the modulus of an annulus, its generalization leads to the idea of the modulus of a plane domain.)
. (Thus, a given annular domain is mapped onto an annulus with a fixed ratio of the radii of the boundary circles. This fact can be taken as another definition of the modulus of an annulus, its generalization leads to the idea of the modulus of a plane domain.)
A generalization of the modulus of an annular domain is the modulus 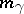 of a prime end (cf. Cluster set; Limit elements)
of a prime end (cf. Cluster set; Limit elements) 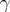 of an open Riemann surface
of an open Riemann surface  relative to a neighbourhood. Depending on whether
relative to a neighbourhood. Depending on whether  is finite or infinite, the prime end has hyperbolic or parabolic type and
is finite or infinite, the prime end has hyperbolic or parabolic type and  either does or does not have a Green function.
either does or does not have a Green function.
For a simply-connected domain  of hyperbolic type the so-called reduced modulus
of hyperbolic type the so-called reduced modulus 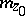 relative to
relative to  is defined as the limit
is defined as the limit
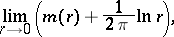 |
where 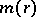 is the modulus of the annular domain
is the modulus of the annular domain 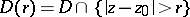 . It turns out that
. It turns out that 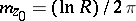 , where
, where 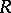 is the conformal radius (cf. Conformal radius of a domain) of
is the conformal radius (cf. Conformal radius of a domain) of  relative to
relative to  .
.
Comments
References
| [a1] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) |
Modulus of an annulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modulus_of_an_annulus&oldid=16103