Non-Euclidean space
A space whose properties are based on a system of axioms other than the Euclidean system. The geometries of non-Euclidean spaces are the non-Euclidean geometries. Depending on the specific axioms from which the non-Euclidean geometries are developed in non-Euclidean spaces, the latter may be classified in accordance with various criteria. On the one hand, a non-Euclidean space may be a finite-dimensional vector space with a scalar product expressible in Cartesian coordinates as
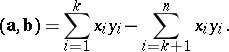 |
In this case one speaks of a pseudo-Euclidean space. On the other hand, a non-Euclidean space can be characterized as an  -dimensional manifold with a certain structure described by a non-Euclidean axiom system.
-dimensional manifold with a certain structure described by a non-Euclidean axiom system.
Non-Euclidean spaces may also be classified from the point of view of their differential-geometric properties as Riemannian spaces of constant curvature (this includes the case of spaces of curvature zero, which are nevertheless topologically distinct from Euclidean spaces).
Comments
References
| [a1] | M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
| [a2] | B. Rosenfeld, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
Non-Euclidean space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-Euclidean_space&oldid=16086