Integral automorphism
From Encyclopedia of Mathematics
The same as a special automorphism, constructed from an automorphism 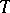 of a measure space
of a measure space 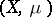 and a function
and a function 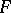 (given on this space and taking values in the positive integers). The term "integral automorphism" is mostly used in the non-Soviet literature.
(given on this space and taking values in the positive integers). The term "integral automorphism" is mostly used in the non-Soviet literature.
Comments
Let  be the measure space
be the measure space 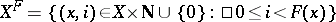 with measure
with measure
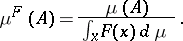 |
Then the integral automorphism 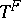 corresponding to
corresponding to 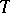 and
and 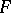 is the automorphism of
is the automorphism of 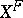 defined by
defined by 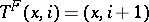 if
if  , and
, and 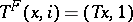 if
if 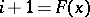 . For more details see [a1] and Special automorphism.
. For more details see [a1] and Special automorphism.
References
| [a1] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) pp. Chapt. 1, Sect. 5 (Translated from Russian) |
How to Cite This Entry:
Integral automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_automorphism&oldid=16070
Integral automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_automorphism&oldid=16070
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article