*-regular ring
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A regular ring (in the sense of von Neumann) admitting an involutory anti-automorphism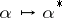 
such that 
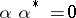implies 
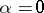. An idempotent 
of a 
-regular ring is called a projector if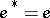 
. Every left (right) ideal of a 
-regular ring is generated by a unique projector. One can thus speak of the lattice of projectors of a 
-regular ring. If this lattice is complete, then it is a continuous geometry. A complemented modular lattice (cf. also Lattice with complements) having a homogeneous basis 
, where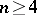 
, is an ortho-complemented lattice if and only if it is isomorphic to the lattice of projectors of some 
-regular ring.
References
| [1] | L.A. Skornyakov, "Complemented modular lattices and regular rings" , Oliver & Boyd (1964) (Translated from Russian) |
| [2] | S.K. Berberian, "Baer  -rings" , Springer (1972) |
| [3] | I. Kaplansky, "Rings of operators" , Benjamin (1968) |
How to Cite This Entry:
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=15998
*-regular ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-regular_ring&oldid=15998
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article