Cartan theorem

Cartan's theorem on the highest weight vector. Let 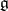be a complex semi-simple Lie algebra, let 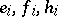, , 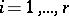be canonical generators of it, that is, linearly-independent generators for which the following relations hold:

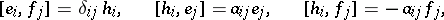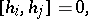where 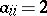, 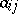are non-positive integers when 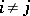, , 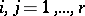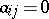implies 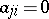, and let 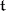be the Cartan subalgebra of 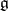which is the linear span of 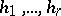. Also let 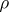be a linear representation of 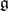in a complex finite-dimensional space 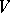. Then there exists a non-zero vector for which

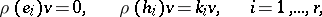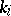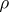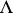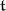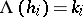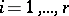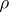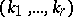where the are certain numbers. This theorem was established by E. Cartan [1]. The vector is called the highest weight vector of the representation and the linear function on defined by the condition , , is called the highest weight of the representation corresponding to . The ordered set is called the set of numerical marks of the highest weight 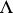. Cartan's theorem gives a complete classification of irreducible finite-dimensional linear representations of a complex semi-simple finite-dimensional Lie algebra. It asserts that each finite-dimensional complex irreducible representation of 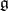has a unique highest weight vector (up to proportionality), and that the numerical marks of the corresponding highest weight are non-negative integers. Two finite-dimensional irreducible representations are equivalent if and only if the corresponding highest weights are the same. Any set of non-negative integers is the set of numerical marks of the highest weight of some finite-dimensional complex irreducible representation.

References

[1]	E. Cartan, "Les tenseurs irréductibles et les groupes linéaires simples et semi-simples" Bull. Sci. Math. , 49 (1925) pp. 130–152
[2]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[3]	, Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955)
[4]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)
[5]	J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French)
[6]	A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970)

References

[a1]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972)

Cartan's theorem in the theory of functions of several complex variables. These are the so-called theorems A and B on coherent analytic sheaves on Stein manifolds, first proved by H. Cartan [1]. Let 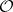be the sheaf of germs of holomorphic functions on a complex manifold 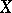. A shea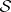f of 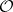-modules on 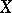is called a coherent analytic sheaf if there exists in a neighbourhood of each point 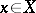an exact sequence of sheaves

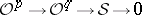for some natural numbers 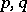. Examples are all locally finitely-generated subsheaves of .

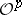Theorem A. Let 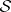be a coherent analytic sheaf on a Stein manifold 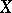. Then there exists for each point 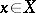a finite number of global sections 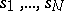of 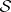such that any element of the fibre 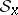is representable in the form

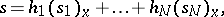with all 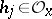. (In other words, locally 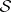is finitely generated over 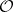by its global sections.)

Theorem B. Let 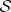be a coherent analytic sheaf on a Stein manifold 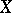. Then all cohomology groups of 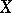of order 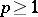with coefficients in 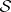are trivial:

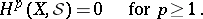These Cartan theorems have many applications. From Theorem A, various theorems can be obtained on the existence of global analytic objects on Stein manifolds. The main corollary of Theorem B is the solvability of the 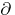-problem: On a Stein manifold, the equation 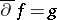with the compatibility condition 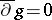is always solvable.

The scheme of application of Theorem B is as follows: If

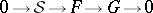is an exact sequence of sheaves on 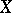, then the sequence

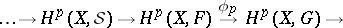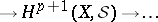is also exact. If 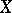is a Stein manifold, then

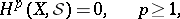and hence, 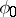is mapping onto and the 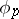, , 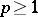are isomorphisms.

Theorem B is best possible: If on a complex manifold 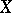the group 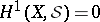for every coherent analytic sheaf 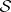, then 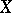is a Stein manifold. Theorems A and B together with their numerous corollaries constitute the so-called Oka–Cartan theory of Stein manifolds. A corollary of these theorems is the solvability on Stein manifolds of all the classical problems of multi-dimensional complex analysis, such as the Cousin problem, the Levi problem, the Poincaré problem and others. Theorems A and B generalize verbatim to Stein spaces (cf. Stein space).

References

[1]	H. Cartan, "Variétés analytiques complexes et cohomologie" R. Remmert (ed.) J.-P. Serre (ed.) , Collected works , Springer (1979) pp. 669–683
[2]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)
[3]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973)

E.M. Chirka

Comments

In [a1] the theory related to Cartan's Theorems A and B is developed on the basis of integral representations, and not on the basis of sheaves, as in [2] or [a2], or on the basis of the Cauchy–Riemann equations, as in [3].

Generalizations to Stein manifolds are in [a2].

See also Cousin problems. For the Poincaré problem (on meromorphic functions), cf. Stein space and Meromorphic function.

References

[a1]	G.M. [G.M. Khenkin] Henkin, J. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1984) (Translated from Russian)
[a2]	H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1977) (Translated from German)
[a3]	S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Sect. 7.1
[a4]	R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. VI, Par. 6