Leibniz formula

for the derivatives of a product

A formula that gives an expression for the -th derivative of the product of two functions in terms of their derivatives of orders 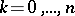(the derivative of order zero is understood to be the function itself). Namely, if the functions 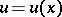and 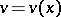have derivatives up to the order inclusive at some point, then at this point their product 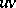has derivatives of the same orders, and for ,

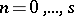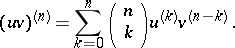This formula was communicated by G. Leibniz in a letter to J. Bernoulli in 1695.