Conditional density
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The density of a conditional distribution. Let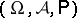 
be a probability space, let 
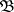be the 
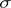-algebra of Borel sets on the line, let 
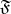be a sub-
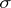-algebra of 
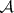, let
 |
be the conditional distribution of 
with respect to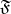 
, and let
 |
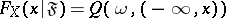be the conditional distribution function of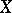 
with respect to 
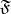. If
 |
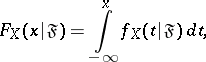then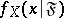 
is called the conditional density of the distribution of 
with respect to the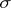 
-algebra 
.
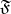If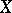 
and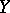 
are random variables, 
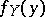is the density of the distribution of 
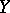and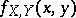 
is the joint density of the distribution of 
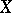and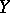 
, then
 |
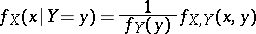defines the conditional density of the distribution of the random variable 
for fixed values 
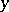of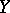 
for which 
.
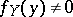References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
How to Cite This Entry:
Conditional density. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conditional_density&oldid=15893
Conditional density. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conditional_density&oldid=15893
This article was adapted from an original article by V.G. Ushakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article