Fibonacci manifold

The Fibonacci manifold 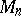, , 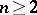is a closed orientable three-dimensional manifold whose fundamental group is the Fibonacci group 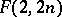(cf. also Orientation). Such manifolds were discovered by H. Helling, A.C. Kim and J. Mennicke [a2] as geometrizations of Fibonacci groups. For 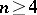, the manifolds 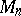are closed hyperbolic three-manifolds (cf. also Hyperbolic metric), 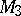is the Euclidean Hantzche–Wendt manifold, and 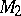is the lens space 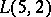(see [a2]).

Many interesting properties of Fibonacci manifolds can be obtained from their relation to links and branched coverings over the three-dimensional sphere 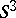, discovered by H.M. Hilden, M.T. Lozano and J.M. Montesinos [a3]. In fact,

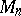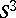1) is the -fold cyclic covering of the three-dimensional sphere , branched over the figure-eight knot (cf. Listing knot), see [a3];

2) 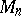can be obtained by Dehn surgery with parameters 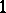and 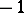on the components of the chain of 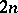linked circles in 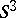, see [a1];

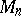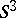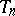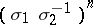3) is the two-fold covering of , branched over the link corresponding to the closed -string braid , see [a9]. The above well-known family 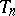of links in 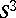includes the figure-eight knot as 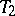, the Borromean rings as 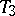, the Turk's head knot 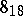as 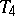, and the knot 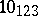as 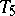(in the notation of [a7]). The last description of 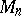also shows that the hyperbolic volumes of the compact Fibonacci manifolds 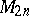, , 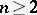coincide with those ones of the (non-compact) link complements 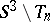, see [a8], [a9]. Also, since the 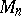are arithmetic if and only if 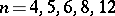(see [a2], [a3] and Arithmetic group), this shows that hyperbolic manifolds with the same volume can be both arithmetic and non-arithmetic, see [a8].

There are several generalizations of Fibonacci manifolds, related to generalizations of the Fibonacci groups, see [a10], [a4], [a5], [a6] and Fibonacci group.

References

[a1]	A. Cavicchioli, F. Spaggiari, "The classification of -manifolds with spines related to Fibonacci groups" , Algebraic Topology, Homotopy and Group Cohomology , Lecture Notes in Mathematics , 1509 , Springer (1992) pp. 50–78
[a2]	H. Helling, A.C. Kim, J. Mennicke, "A geometric study of Fibonacci groups" J. Lie Theory , 8 (1998) pp. 1–23
[a3]	H.M. Hilden, M.T. Lozano, J.M. Montesinos, "The arithmeticity of the figure-eight knot orbifolds" B. Apanasov (ed.) W. Neumann (ed.) A. Reid (ed.) L. Siebenmann (ed.) , Topology'90 , de Gruyter (1992) pp. 169–183
[a4]	A.C. Kim, A. Vesnin, "The fractional Fibonacci groups and manifolds" Sib. Math. J. , 38 (1997) pp. 655–664
[a5]	C. Maclachlan, "Generalizations of Fibonacci numbers, groups and manifolds" A.J. Duncan (ed.) N.D. Gilbert (ed.) J. Howie (ed.) , Combinatorial and Geometric Group Theory (Edinburgh, 1993) , Lecture Notes , 204 , London Math. Soc. (1995) pp. 233–238
[a6]	C. Maclachlan, A.W. Reid, "Generalized Fibonacci manifolds" Transformation Groups , 2 (1997) pp. 165–182
[a7]	D. Rolfson, "Knots and links" , Publish or Perish (1976)
[a8]	A.Yu. Vesnin, A.D. Mednykh, "Hyperbolic volumes of Fibonacci manifolds" Sib. Math. J. , 36 : 2 (1995) pp. 235–245
[a9]	A.Yu. Vesnin, A.D. Mednykh, "Fibonacci manifolds as two-fold coverings over the three-dimensional sphere and the Meyerhoff–Neumann conjecture" Sib. Math. J. , 37 : 3 (1996) pp. 461–467
[a10]	B.N. Apanasov, "Conformal geometry of discrete groups and manifolds" , de Gruyter (2000)