Euler criterion
From Encyclopedia of Mathematics
If an integer  is not divisible by a prime number
is not divisible by a prime number 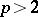 , then the congruence
, then the congruence
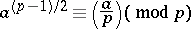 |
holds, where  is the Legendre symbol. Thus, the Euler criterion gives a necessary and sufficient condition for a number
is the Legendre symbol. Thus, the Euler criterion gives a necessary and sufficient condition for a number 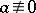 (
(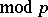 ) to be a quadratic residue or non-residue modulo
) to be a quadratic residue or non-residue modulo 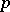 . It was proved by L. Euler in 1761 (see [1]).
. It was proved by L. Euler in 1761 (see [1]).
Euler also obtained a more general result: A number  (
(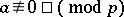 ) is a residue of degree
) is a residue of degree  modulo a prime number
modulo a prime number 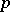 if and only if
if and only if
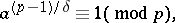 |
where 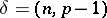 .
.
Both these assertions carry over easily to the case of a finite field.
References
| [1] | L. Euler, "Adnotationum ad calculum integralem Euleri" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 12 , Teubner (1914) pp. 493–538 |
| [2] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 |
How to Cite This Entry:
Euler criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_criterion&oldid=15846
Euler criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_criterion&oldid=15846
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article