Form of an (algebraic) structure

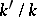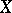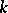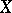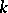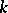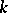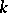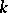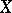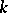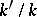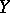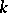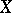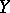Let be an extension of fields, and let be some "object" defined over . For example, could be a vector space together with a quadratic form, a Lie algebra over , an Azumaya algebra over , a variety over , an algebraic group over , a representation of a finite group in a -vector space, etc. A form of over , more precisely, a -form, is an object of the same type over such that and become isomorphic over 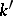, i.e. after extending scalars from 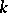to 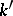the objects 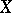and 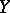become isomorphic. Let 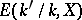denote the set of 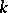-isomorphism classes of forms of 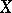. If now 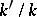is a Galois extension, then under suitable circumstances one has a bijection between 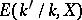and the Galois cohomology group 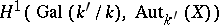(cf. Galois cohomology), where 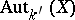is the group of automorphisms over 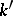of 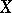. Consider, for instance, the case where the object 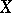is a finite-dimensional algebra 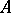over 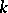. 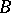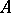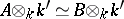Then is a form of if as 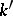-algebras. Let 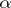be an automorphism of 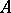over 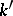, i.e. an isomorphism of 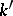-algebras 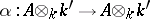, and let 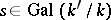. Then 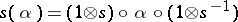is another 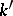-automorphism of 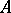. This defines the action of 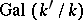on 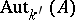. Now let 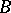be a form of 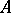. The set of 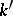-isomorphisms 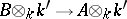is naturally a principal homogeneous space over 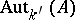and thus defines an element of 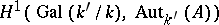. This mapping is a bijection in this case. More generally one has such a bijection for the case that the structure 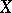is a vector space 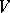together with a 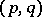-tensor (the previous case corresponds to the case of a 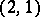-tensor). (To prove surjectivity one needs the generalization of Hilbert's theorem 90: 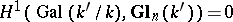.) For the case of algebraic groups over 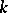cf. Form of an algebraic group.

For the case of algebraic varieties over 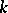one has that 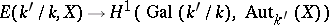is injective and that it is bijective if 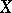is quasi-projective.

The concept of forms makes sense in a far more general setting, e.g. in any category with base change, i.e. with fibre products. Indeed, let 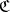be such a category, and 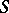an object in 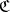. An object over 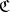is a morphism in 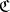, 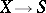. Let 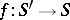be a morphism in 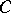. Base change from 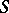to 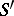gives the pullback (fibre product) 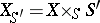defined by the Cartesian square

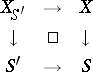(In case 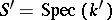, 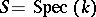and 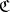is, for instance, the category of (affine) schemes this corresponds to extending scalars.)

An object 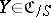is now an -form of 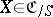if the objects 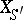and 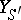are isomorphic over 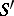. For an even more general setting cf. [a2].

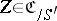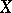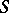A related problem (to that of forms) is the subject of descent theory. In the setting of a category with base change as above this theory is concerned with the question: Given , does there exists an over such that 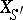is isomorphic over 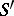to 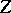, and what properties must 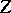satisfy for this to be the case.

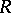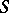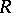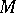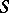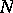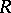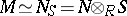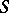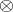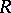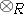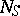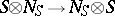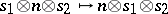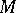Below this question is examined in the following setting: is a commutative algebra (with unit element) and is a commutative -algebra. Given a module over the question is whether there exists a module over such that (as -modules). Below all tensor products are tensor products over : . If is of the form there is a natural isomorphism of modules given by . Let be an 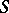-module. A descent datum on 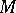is an isomorphism of modules 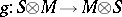such that 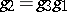. Here 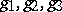are the three natural 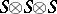-module homomorphisms defined by 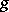, where 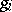is the identity on factor 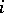and given by 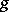on the other two components:

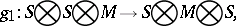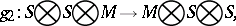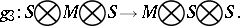The faithfully flat descent theorem now says that if 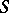is faithfully flat over 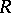and 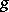is a descent datum for 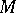over 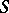, then there exists an 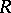-module 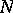and an isomorphism 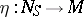such that the following diagram commutes

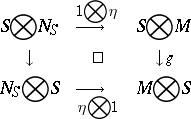where the left vertical arrow is the descent datum on 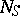described above. Moreover, the pair 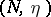is uniquely defined by this property. One defines 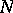by an invariance property: 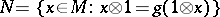(which is like invariance under the Galois group in the case of Galois descent).

There is a similar theorem for descent of algebras over .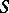

In algebraic geometry one has for instance the following descent theorem (a globalization of the previous one for algebras). For a morphism of schemes 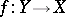, consider the fibre products 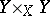and 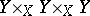and let 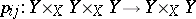be the projections 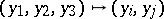, 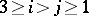; and 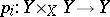the projections 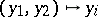, 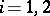. Let 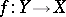be faithfully flat and compact. Then to give a scheme 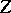affine over 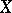is the same as to give a scheme 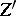affine over 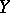together with an isomorphism 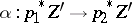such that .

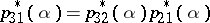The theory of descent is quite general and includes such matters as specifying a section of a sheaf by local sections and the construction of locally trivial fibre bundles by glueing together trivial bundles 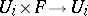over the elements of an open covering 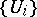of 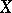. Indeed, let 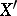be the disjoint union of the 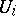and 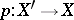the natural projection. Giving glueing data 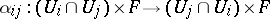is the same as giving an isomorphism 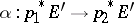, where 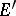is the trivial vector bundle 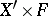with fibre 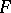and the compatibility of the glueing data amounts to the condition .

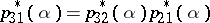For a treatment of forms of Lie algebras (over fields) cf. [a7], for Lie algebras over characteristic zero fields and the modular case (i.e. over fields of characteristic 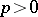) cf. [a5]. For a quite comprehensive treatment of descent and forms cf. [a1].

A form of an object is also occasionally called a twisted form.

In the case of descent with respect to a Galois field extension 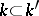(or 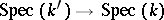) one speaks of Galois descent.

References

[a1]	M.-A. Knus, M. Ojanguren, "Théorie de la descent et algèbres d'Azumaya" , Springer (1974)
[a2]	A. Grothendieck, "Revêtements étales et groupe fondamental" , SGA 1960–1961 , Exp. VI: Categories fibrées et descente , IHES (1961)
[a3]	J.P. Murre, "Lectures on an introduction to Grothendieck's theory of the fundamental group." , Tata Inst. Fund. Res. (1967) pp. Chapt. VII
[a4]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1973)
[a5]	G.B. Seligman, "Modular Lie algebras" , Springer (1967) pp. Chapt. IV
[a6]	J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) pp. Chapt. V, Sect. 20
[a7]	N. Jacobson, "Lie algebras" , Dover, reprint (1979) pp. Chapt. X ((also: Dover, reprint, 1979))