Quasi-solution
A generalized solution of a certain ill-posed problem that (under sufficiently general conditions) satisfies, in contrast to a proper solution, the condition of being well-posed in the sense of Hadamard.
Let 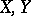 be metric spaces, let
be metric spaces, let 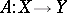 and let
and let 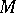 be a subset of
be a subset of 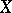 . A quasi-solution of the equation
. A quasi-solution of the equation
 | (1) |
on the set 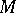 for given
for given 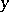 in
in 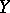 is an element
is an element 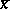 in
in 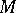 that minimizes the residual
that minimizes the residual 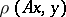 for
for  in
in 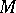 . If equation (1) has a proper solution
. If equation (1) has a proper solution 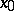 on
on 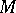 , then
, then 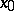 is also quasi-solution.
is also quasi-solution.
The dependence of the set of quasi-solutions on 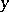 is conveniently represented as a superposition of two mappings:
is conveniently represented as a superposition of two mappings:
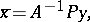 |
where 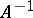 is the (generally multi-valued) inverse of
is the (generally multi-valued) inverse of  and
and 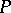 is the metric projection operator in
is the metric projection operator in 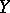 onto the set
onto the set 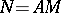 . This superposition enables one to reduce the study of the properties of quasi-solutions to that of the mappings
. This superposition enables one to reduce the study of the properties of quasi-solutions to that of the mappings  and
and 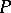 . For example, if
. For example, if 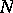 is a Chebyshev set and
is a Chebyshev set and 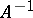 is single-valued and continuous on
is single-valued and continuous on 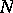 , then the problem of finding a quasi-solution is well-posed. If
, then the problem of finding a quasi-solution is well-posed. If 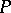 or
or 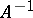 is many-valued, then stability of the set
is many-valued, then stability of the set 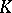 can be formulated in terms of
can be formulated in terms of 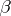 -continuity (continuity of set-valued functions).
-continuity (continuity of set-valued functions).
 and
and 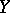 are generally taken to be normed linear spaces, which enables one to obtain more complete and definitive results. Then the problem of finding quasi-solutions is well-posed if
are generally taken to be normed linear spaces, which enables one to obtain more complete and definitive results. Then the problem of finding quasi-solutions is well-posed if 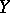 is strictly convex,
is strictly convex, 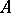 is a continuous invertible linear operator and
is a continuous invertible linear operator and 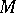 is a convex compactum. There are a number of other combinations of conditions that ensure the well-posedness of the problem of finding quasi-solutions, in which some conditions are strengthened while others are weakened (for example,
is a convex compactum. There are a number of other combinations of conditions that ensure the well-posedness of the problem of finding quasi-solutions, in which some conditions are strengthened while others are weakened (for example, 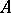 is a closed linear operator but
is a closed linear operator but 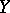 is a Hilbert space).
is a Hilbert space).
There exists a number of methods for determining sets 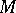 that guarantee an effective determination of quasi-solutions. One of the most widespread methods consists in the following: One considers a third space
that guarantee an effective determination of quasi-solutions. One of the most widespread methods consists in the following: One considers a third space 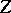 (all or some of the spaces
(all or some of the spaces 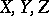 may coincide) and a linear operator
may coincide) and a linear operator 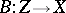 for which
for which 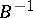 is unbounded. One takes for the set
is unbounded. One takes for the set 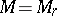 the image of a ball
the image of a ball
 |
In this form the problem of finding a quasi-solution is a mathematical programming problem: To minimize the functional
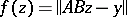 |
subject to 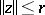 . For Hilbert spaces
. For Hilbert spaces  and
and 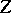 one obtains a quadratic programming problem.
one obtains a quadratic programming problem.
In the case of well-posedness of quasi-solutions, of great importance in applications are stability estimates, in which the dependence of 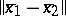 on
on 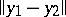 is given. If the method for determining the set
is given. If the method for determining the set 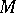 is as described above, then stability of a quasi-solution is characterized by the function
is as described above, then stability of a quasi-solution is characterized by the function
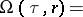 |
 |
The following relation holds:
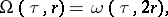 |
where  is the solution of the extremal problem
is the solution of the extremal problem  .
.
For Hilbert spaces 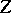 and
and 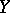 there are expressions for
there are expressions for  in closed form.
in closed form.
References
| [1] | V.K. Ivanov, "On linear problems which are not well-posed" Soviet Math. Dokl. , 4 : 3 (1962) pp. 981–983 Dokl. Akad. Nauk SSSR , 145 : 2 (1962) pp. 270–272 |
| [2] | V.K. Ivanov, "On ill-posed problems" Mat. Sb. , 61 : 2 (1962) pp. 211–223 (In Russian) |
| [3] | O.A. Liskovets, "Stability of quasi-solutions of equations with a closed operator" Diff. Eq. , 7 : 9 (1971) pp. 1300–1303 Differentsial. Uravn. , 7 : 9 (1971) pp. 1707–1709 |
| [4] | V.A. Morozov, "Linear and nonlinear ill-posed problems" J. Soviet Math. , 4 : 6 (1975) pp. 706–755 Itogi Nauk. i Tekhn. Mat. Anal. , 11 (1973) pp. 129–178 |
| [5] | A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solution of ill-posed problems" , Wiley (1977) (Translated from Russian) |
| [6] | V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Computing methods of higher mathematics" , 1–2 , Minsk (1972–1975) (In Russian) |
Comments
Frequently the operator 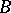 is such that
is such that  is a differential operator. On a suitable space,
is a differential operator. On a suitable space, 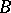 is then a compact operator, so that the set
is then a compact operator, so that the set  is a compactum.
is a compactum.
References
| [a1] | B. Hofmann, "Regularization for applied inverse and ill-posed problems" , Teubner (1986) |
| [a2] | C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind" , Pitman (1984) |
| [a3] | J. Baumeister, "Stable solution of inverse problems" , Vieweg (1987) |
| [a4] | M.Z. Nashed (ed.) , Genealized inverses and applications , Acad. Press (1976) |
| [a5] | V.A. Morozov, "Methods for solving incorrectly posed problems" , Springer (1984) (Translated from Russian) |
Quasi-solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-solution&oldid=15713