Complete group
From Encyclopedia of Mathematics
A group  whose centre (cf. Centre of a group) is trivial (that is,
whose centre (cf. Centre of a group) is trivial (that is,  is a so-called group without centre) and for which all automorphisms are inner (see Inner automorphism). The automorphism group of a complete group
is a so-called group without centre) and for which all automorphisms are inner (see Inner automorphism). The automorphism group of a complete group  is isomorphic to
is isomorphic to  itself (the term "complete" is related to this property). Examples of complete groups are the symmetric groups
itself (the term "complete" is related to this property). Examples of complete groups are the symmetric groups  when
when  (cf. Symmetric group). If a group
(cf. Symmetric group). If a group  contains a normal subgroup which is complete, then
contains a normal subgroup which is complete, then  decomposes into a direct product
decomposes into a direct product  of a subgroup
of a subgroup  and its centralizer in
and its centralizer in 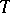 .
.
References
| [1] | M.I. Kargapolov, Yu.I. Merzlyakov, "Fundamentals of group theory" , Moscow (1982) (In Russian) |
| [2] | M. Hall jr., "Group theory" , Chelsea (1976) |
How to Cite This Entry:
Complete group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_group&oldid=15667
Complete group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_group&oldid=15667
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article