Egorov system of surfaces

A tri-orthogonal system 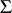consisting of so-called potential surfaces (cf. Potential net), named after D.F. Egorov, who in 1901 (see [1]) considered their general theory in detail (under the name of potential systems) and gave numerous examples of systems of this type. An Egorov system 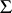can be defined as a system admitting a (one-parameter) group of transformations taking 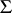into itself in such a way that the normals at corresponding points of 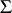remain parallel. The stationary flow of a fluid with a velocity potential and carrying the surfaces of an Egorov system provides a mechanical interpretation of this group.

Let

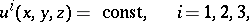be the equations of the surfaces forming an Egorov system ; let be the Lamé coefficients appearing in the expression for the square of the line element of the space in the curvilinear coordinates :

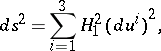let 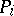be the distance between the origin and the three tangent planes to 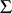, let 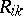be the principal radii of curvature of the surfaces 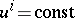, corresponding to the principal direction 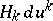, and let 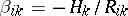be the quantities appearing in the expression for the line elements 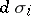of the spherical images (cf. Spherical map) of the surfaces:

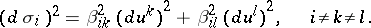The functions 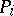and 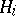satisfy the same system of equations:

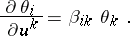The solutions of these equations define two other Egorov systems, 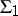and 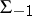, with the same spherical images, for which

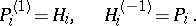Continuing this transformation in both directions gives a series of Egorov systems (the Egorov series)

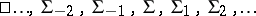with the same spherical image, in which each 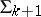is obtained from the previous 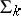by the formula

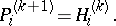In general, the search for the spherical image of an Egorov system 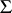reduces to the investigation of a potential system on the sphere: Any such system may be taken as the spherical image of one of the three families forming .

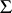An Egorov system 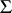is characterized by the fact that

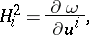where 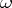is a function having the meaning of velocity potential for the corresponding flow, that is, 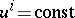are the potential surfaces. Thus, for any potential surface 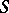, there is an Egorov system 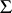containing 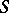. The tangent to the line of intersection of any surface 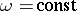with the surface 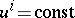at any point is parallel to the ray 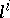joining the centres of geodesic curvature of the lines of curvature of the surface 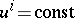; at each point of space the three rays 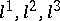are parallel to a common plane — the tangent plane to the surface 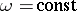, and the osculating planes of the coordinate lines pass through a common straight line. The quantities 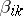and 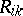for an Egorov system satisfy the relations:

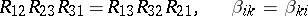(the symmetry of 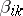is also a necessary and sufficient condition for a tri-orthogonal system to be an Egorov system).

References

[1]	D.F. Egorov, "Papers in differential geometry" , Moscow (1970) (In Russian)