Glueing
Glueing in differential topology, algebraic and analytic geometry, etc. is a frequently used method to construct global objects such as varieties, schemes, differentiable manifolds, vector bundles, sheaves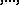 from local pieces from some category of local models together with glueing data.
from local pieces from some category of local models together with glueing data.
Consider, for example, the case of differentiable manifolds of dimension  . In this case the local model category consists of open sets in
. In this case the local model category consists of open sets in 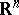 and differentiable mappings. A local-pieces-and-glueing-data description of an
and differentiable mappings. A local-pieces-and-glueing-data description of an  -dimensional differentiable manifold
-dimensional differentiable manifold  now consists of the following:
now consists of the following:
i) a collection of open subsets 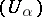 of
of 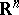 indexed by
indexed by 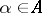 ;
;
ii) for each 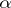 and
and 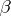 open subsets
open subsets 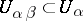 and
and 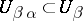 together with a diffeomorphism
together with a diffeomorphism  .
.
The glueing data  are subject to the following consistency conditions:
are subject to the following consistency conditions:
iii) 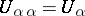 ,
, 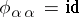 ;
;
iv) 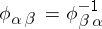 ;
;
v) 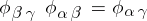 on
on 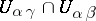 .
.
From these data one constructs a locally Euclidean space  by taking the disjoint union,
by taking the disjoint union, 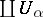 , of the
, of the 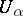 modulo the equivalence relation
modulo the equivalence relation 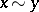 if
if 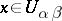 ,
,  and
and 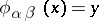 for some
for some 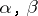 . If the resulting topological space
. If the resulting topological space 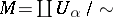 is Hausdorff and paracompact, then a differentiable manifold is obtained. Both these properties do not follow from the construction. Local coordinate systems are obtained from (the inverses of) the natural mappings
is Hausdorff and paracompact, then a differentiable manifold is obtained. Both these properties do not follow from the construction. Local coordinate systems are obtained from (the inverses of) the natural mappings  .
.
For (pre-)schemes the local model category is that of affine schemes 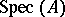 and morphisms of schemes between them. Cf. Scheme. Here also global separation properties must be added to obtain a scheme. For vector bundles the local model category is that of trivial vector bundles
and morphisms of schemes between them. Cf. Scheme. Here also global separation properties must be added to obtain a scheme. For vector bundles the local model category is that of trivial vector bundles 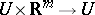 ,
, 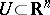 , and vector bundle morphisms between such trivial vector bundles, i.e. differentiable mappings
, and vector bundle morphisms between such trivial vector bundles, i.e. differentiable mappings 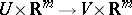 of the form
of the form  , where
, where 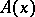 is an
is an 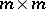 matrix smoothly depending on
matrix smoothly depending on  . Cf. Vector bundle.
. Cf. Vector bundle.
If  is a differentiable manifold with a covering
is a differentiable manifold with a covering  by coordinate neighbourhoods and corresponding coordinate systems
by coordinate neighbourhoods and corresponding coordinate systems  , then the corresponding local-pieces-and-glueing-data description of
, then the corresponding local-pieces-and-glueing-data description of 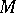 is as follows. The local pieces are the
is as follows. The local pieces are the 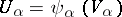 . The open subsets
. The open subsets 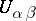 are equal to the
are equal to the  and the glueing data
and the glueing data  are the mappings
are the mappings 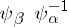 restricted to
restricted to  . Thus, the description of a manifold by means of an atlas and the description by means of local pieces and glueing data are quite close to one another.
. Thus, the description of a manifold by means of an atlas and the description by means of local pieces and glueing data are quite close to one another.
References
| [a1] | A. Grothendieck, "Elements de géométrie algébrique I" , IHES (1960) pp. Sect. 0.4.1.7 |
| [a2] | M. Hazewinkel, "A tutorial introduction to differentiable manifolds and calculus on differentiable manifolds" W. Schiehlen (ed.) W. Wedig (ed.) , Analysis and estimation of stochastic mechanical systems , Springer (Wien) (1988) pp. 316–340 |
Glueing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Glueing&oldid=15657