A functor "measuring" the deviation of a given functor from being exact. Let  be an additive functor from the product of the category of
be an additive functor from the product of the category of  -modules with the category of
-modules with the category of  -modules into the category of
-modules into the category of  -modules that is covariant in the first argument and contravariant in the second argument. From an injective resolution
-modules that is covariant in the first argument and contravariant in the second argument. From an injective resolution  of
of  and a projective resolution
and a projective resolution  of
of  one obtains a doubly-graded complex
one obtains a doubly-graded complex  . The homology of the associated single complex
. The homology of the associated single complex  does not depend on the choice of resolutions, has functorial properties and is called the right derived functor
does not depend on the choice of resolutions, has functorial properties and is called the right derived functor  of
of  . The basic property of a derived functor is the existence of long exact sequences
. The basic property of a derived functor is the existence of long exact sequences
induced by short exact sequences
The left derived functor is defined analogously. The derived functor of 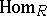 is denoted by
is denoted by  . The group
. The group 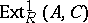 classifies extensions of
classifies extensions of 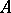 with kernel
with kernel  up to equivalence (cf. Baer multiplication; Cohomology of algebras).
up to equivalence (cf. Baer multiplication; Cohomology of algebras).
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | S. MacLane, "Homology" , Springer (1963) |
The above article does not explain the sense in which 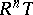 measures the deviation of
measures the deviation of  from being exact. The point is that if
from being exact. The point is that if  is left exact (i.e. preserves the exactness of sequences of the form
is left exact (i.e. preserves the exactness of sequences of the form  in the fist variable and of the form
in the fist variable and of the form  in the second), then
in the second), then  is naturally isomorphic to
is naturally isomorphic to 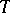 ; if further
; if further 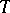 is exact, then
is exact, then  for all
for all 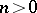 . Derived functors may also be defined for additive functors of a single variable between module categories, or, more generally, between arbitrary Abelian categories, provided the necessary injective or projective resolutions exist in the domain category.
. Derived functors may also be defined for additive functors of a single variable between module categories, or, more generally, between arbitrary Abelian categories, provided the necessary injective or projective resolutions exist in the domain category.
How to Cite This Entry:
Derived functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derived_functor&oldid=15566
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article be an additive functor from the product of the category of
be an additive functor from the product of the category of  -modules with the category of
-modules with the category of  -modules into the category of
-modules into the category of  -modules that is covariant in the first argument and contravariant in the second argument. From an injective resolution
-modules that is covariant in the first argument and contravariant in the second argument. From an injective resolution  of
of  and a projective resolution
and a projective resolution  of
of  one obtains a doubly-graded complex
one obtains a doubly-graded complex  . The homology of the associated single complex
. The homology of the associated single complex  does not depend on the choice of resolutions, has functorial properties and is called the right derived functor
does not depend on the choice of resolutions, has functorial properties and is called the right derived functor  of
of  . The basic property of a derived functor is the existence of long exact sequences
. The basic property of a derived functor is the existence of long exact sequences
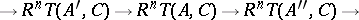
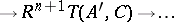
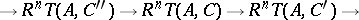
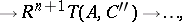
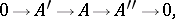
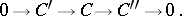
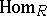 is denoted by
is denoted by  . The group
. The group 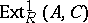 classifies extensions of
classifies extensions of 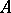 with kernel
with kernel  up to equivalence (cf. Baer multiplication; Cohomology of algebras).
up to equivalence (cf. Baer multiplication; Cohomology of algebras).
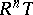 measures the deviation of
measures the deviation of  from being exact. The point is that if
from being exact. The point is that if  is left exact (i.e. preserves the exactness of sequences of the form
is left exact (i.e. preserves the exactness of sequences of the form  in the fist variable and of the form
in the fist variable and of the form  in the second), then
in the second), then  is naturally isomorphic to
is naturally isomorphic to 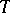 ; if further
; if further 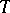 is exact, then
is exact, then  for all
for all 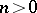 . Derived functors may also be defined for additive functors of a single variable between module categories, or, more generally, between arbitrary Abelian categories, provided the necessary injective or projective resolutions exist in the domain category.
. Derived functors may also be defined for additive functors of a single variable between module categories, or, more generally, between arbitrary Abelian categories, provided the necessary injective or projective resolutions exist in the domain category.