Perturbation of a linear system
The mapping 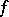 in the system of ordinary differential equations
in the system of ordinary differential equations
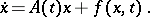 | (1) |
A perturbation is usually assumed to be small in some sense, for example
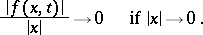 | (2) |
The solution 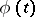 of the perturbed system (1) and the solution
of the perturbed system (1) and the solution  of the linear system
of the linear system
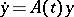 | (3) |
with the same initial value 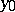 at
at 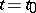 , are connected by the relation
, are connected by the relation
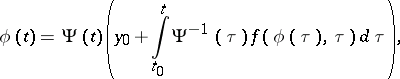 |
known as the formula of variation of constants, where 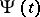 is the fundamental matrix of the linear system (3).
is the fundamental matrix of the linear system (3).
It was shown by A.M. Lyapunov [1] that the trivial solution of the system (1) is asymptotically stable (cf. Asymptotically-stable solution) if relation (2) is valid uniformly in 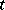 , the matrix
, the matrix 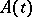 is constant and all real parts of the eigen values of
is constant and all real parts of the eigen values of 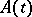 are negative; if only one such real part is positive, the trivial solution is not stable.
are negative; if only one such real part is positive, the trivial solution is not stable.
The study of the periodic solution 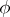 of the system
of the system 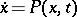 , describing an oscillating process, reduces in the general case by the transformation
, describing an oscillating process, reduces in the general case by the transformation 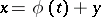 to the study of a perturbed linear system, the right-hand side of which is periodic in
to the study of a perturbed linear system, the right-hand side of which is periodic in 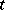 [3].
[3].
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [3] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
Comments
Results of this type are usually called Poincaré–Lyapunov theorems. There are several extensions, described, e.g., in [a1]. A recent tutorial text containing these matters is [a2].
References
| [a1] | M. Roseau, "Vibrations non linéaires et théorie de la stabilité" , Springer (1966) |
| [a2] | F. Verhulst, "Nonlinear differential equations and dynamical systems" , Springer (1989) |
Perturbation of a linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perturbation_of_a_linear_system&oldid=15561