Möbius function

An arithmetic function of natural argument: , 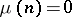if is divisible by the square of a prime number, otherwise , where is the number of prime factors of the number . This function was introduced by A. Möbius in 1832.

The Möbius function is a multiplicative arithmetic function; if 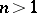. It is used in the study of other arithmetic functions; it appears in inversion formulas (see, e.g. Möbius series). The following estimate is known for the mean value of the Möbius function [2]:

where is a constant. The fact that the mean value tends to zero as 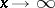implies an asymptotic law for the distribution of prime numbers in the natural series.

References

[1]	I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)
[2]	A. Walfisz, "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft. (1963)

Comments

The multiplicative arithmetic functions form a group under the convolution product 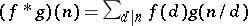. The Möbius function is in fact the inverse of the constant multiplicative function 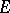(defined by 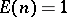for all ) under this convolution product. From this there follows many "inversion formulas" , cf. e.g. Möbius series.

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979)