Complete integral
The solution 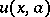 ,
, 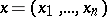 ,
, 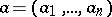 , of a first-order partial differential equation
, of a first-order partial differential equation
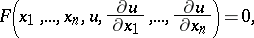 | (1) |
that depends on  parameters
parameters  and in the relevant region satisfies the condition
and in the relevant region satisfies the condition
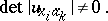 |
If 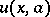 is considered as an
is considered as an  -parameter family of solutions, then the envelope of any
-parameter family of solutions, then the envelope of any 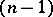 -parameter subfamily distinguished by the condition
-parameter subfamily distinguished by the condition 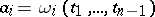 ,
, 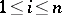 , is a solution to (1). Then the lines of contact between the surfaces given by the complete integral and the envelope are characteristics of (1). A complete integral can be used to describe the solution of the characteristic system of the ordinary differential equations corresponding to (1), and thus enables one to reverse Cauchy's method, which reduces the solution of (1) to that of the characteristic system. This approach is used in analytical mechanics, where one has to find the solution of a canonical system of ordinary differential equations
, is a solution to (1). Then the lines of contact between the surfaces given by the complete integral and the envelope are characteristics of (1). A complete integral can be used to describe the solution of the characteristic system of the ordinary differential equations corresponding to (1), and thus enables one to reverse Cauchy's method, which reduces the solution of (1) to that of the characteristic system. This approach is used in analytical mechanics, where one has to find the solution of a canonical system of ordinary differential equations
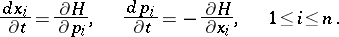 | (2) |
This system is a characteristic one for the Jacobi equation
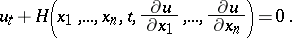 | (3) |
If the complete integral 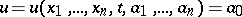 for (3) is known, then the
for (3) is known, then the 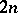 integrals of the canonical system (2) are given by the equations
integrals of the canonical system (2) are given by the equations 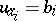 ,
, 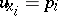 ,
, 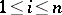 , where
, where 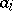 and
and 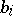 are arbitrary constants.
are arbitrary constants.
Comments
The Jacobi equation is usually called the (time-dependent) Hamilton–Jacobi equation (see also Hamiltonian system).
References
| [a1] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a2] | B.A. Dubrovin, A.T. Fomenko, S.P. Novikov, "Modern geometry - methods and applications" , 1 , Springer (1984) (Translated from Russian) |
Complete integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_integral&oldid=15444