Relative homological algebra

A homological algebra associated with a pair of Abelian categories and a fixed functor (cf. Abelian category). The functor is taken to be additive, exact and faithful. A short exact sequence of objects of ,

is said to be admissible if the exact sequence

splits in 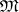(cf. Split sequence). By means of the class of admissible exact sequences, the class of -projective (respectively, 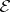-injective) objects is defined as the class of those objects 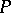(respectively, 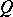) for which the functor 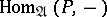(respectively, 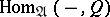) is exact on the admissible short exact sequences.

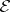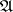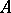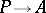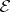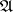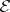Any projective object of is -projective, although this does not mean that in there are enough relative projective objects (i.e. that for any object from , an admissible epimorphism of a certain -projective object of exists). If contains enough -projective or -injective objects, then the usual constructions of homological algebra make it possible to construct derived functors in this category, which are called relative derived functors.

Examples. Let be the category of -modules over an associative ring 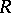with a unit, let be the category of Abelian groups and let be the functor which "forgets" the module structure. In this case all exact sequences are admissible, and as a result the "absolute" (i.e. usual) homological algebra is obtained.

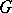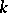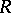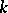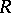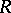If is a group, then every -module is, in particular, an Abelian group. If is an algebra over a commutative ring , then every -module is a -module. If and are rings and , then every -module is an 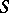-module. In all these cases there is a functor from one Abelian category into the other defining the relative derived functors.

References

[1]	S. MacLane, "Homology" , Springer (1963)
[2]	J.C. Moore, S. Eilenberg, "Foundations of relative homological algebra" , Amer. Math. Soc. (1965)