Gauss semi-group
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A commutative semi-group with unit satisfying the cancellation law, in which any non-invertible element 
is decomposable into a product of irreducible elements (i.e. elements that cannot be represented as a product of non-invertible factors); moreover, for each two such decompositions
 |
one has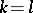 
and, possibly after renumbering the factors, also
 |
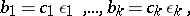where 
are invertible elements. Typical examples of Gauss semi-groups include the multiplicative semi-group of non-zero integers, and that of non-zero polynomials in one unknown over a field. Any two elements of a Gauss semi-group have a highest common divisor.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
How to Cite This Entry:
Gauss semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_semi-group&oldid=15403
Gauss semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_semi-group&oldid=15403
This article was adapted from an original article by L.N. Shevrin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article