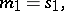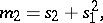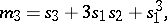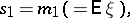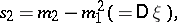A numerical characteristic of random variables related to the concept of a moment of higher order. If  is a random vector,
is a random vector,  is its characteristic function,
is its characteristic function,  ,
,  ,
,
and if for some  the moments
the moments  ,
,  , then the (mixed) moments
, then the (mixed) moments
exist for all non-negative integers  such that
such that  . Under these conditions,
. Under these conditions,
where  , and for sufficiently small
, and for sufficiently small  the principal value of
the principal value of  can be represented by Taylor's formula as
can be represented by Taylor's formula as
where the coefficients  are called the (mixed) semi-invariants, or cumulants, of order
are called the (mixed) semi-invariants, or cumulants, of order  of the vector
of the vector  . For independent random vectors
. For independent random vectors  and
and  ,
,
that is, the semi-invariant of a sum of independent random vectors is the sum of their semi-invariants. This is the reason for the term "semi-invariant" , which reflects the additive property of independent variables (but, in general, the property does not hold for dependent variables).
The following formulas, connecting moments and semi-invariants, hold:
where  denotes summation over all ordered sets of non-negative integer vectors
denotes summation over all ordered sets of non-negative integer vectors  ,
, 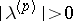 , with as sum the vector
, with as sum the vector  . (Here
. (Here  is defined as
is defined as 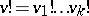 , and similarly for the
, and similarly for the  .) In particular, if
.) In particular, if  is a random variable
is a random variable  ,
,  , and
, and  , then
, then
and
References
| [1] | V.P. Leonov, A.N. Shiryaev, "On a method of calculation of semi-invariants" Theory Probab. Appl. , 4 : 3 (1959) pp. 319–329 Teor. Veroyatnost. i Primen. , 4 : 3 (1959) pp. 342–355 |
| [2] | A.N. Shiryaev, "Probability" , Springer (1984) (Translated from Russian) |
References
| [a1] | A. Stuart, J.K. Ord, "Kendall's advanced theory of statistics" , Griffin (1987) |
| [a2] | L. Schmetterer, "Introduction to mathematical statistics" , Springer (1974) pp. Chapt. 1, §42 (Translated from German) |
| [a3] | A. Rényi, "Probability theory" , North-Holland (1970) pp. Chapt. 3, §15 |
How to Cite This Entry:
Semi-invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-invariant&oldid=15401
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article is a random vector,
is a random vector,  is its characteristic function,
is its characteristic function,  ,
,  ,
,
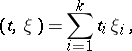
 the moments
the moments  ,
,  , then the (mixed) moments
, then the (mixed) moments
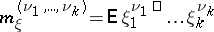
 such that
such that  . Under these conditions,
. Under these conditions,


 , and for sufficiently small
, and for sufficiently small  the principal value of
the principal value of  can be represented by Taylor's formula as
can be represented by Taylor's formula as

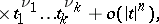
 are called the (mixed) semi-invariants, or cumulants, of order
are called the (mixed) semi-invariants, or cumulants, of order  of the vector
of the vector  . For independent random vectors
. For independent random vectors  and
and  ,
,
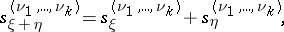
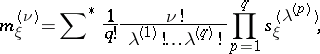
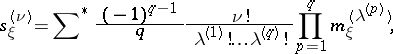
 denotes summation over all ordered sets of non-negative integer vectors
denotes summation over all ordered sets of non-negative integer vectors  ,
, 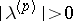 , with as sum the vector
, with as sum the vector  . (Here
. (Here  is defined as
is defined as 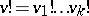 , and similarly for the
, and similarly for the  .) In particular, if
.) In particular, if  is a random variable
is a random variable  ,
,  , and
, and  , then
, then