Complete probability formula

A relationship enabling one to calculate the unconditional probability of an event via its conditional probabilities with respect to events forming a complete set of alternatives.

More precisely, let be a probability space, and let be events for which for , ,

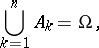and for all . Then one has the complete probability formula:

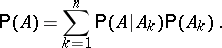The complete probability formula also holds when the number of events 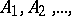is infinite.

The complete probability formula holds for mathematical expectations. Let , , 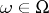be a random variable on 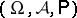, let 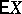be its mathematical expectation and the conditional mathematical expectations with respect to events 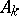which form a complete set of alternatives. Then

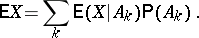Comments

A complete set of alternatives is also called a partition of the sample space. A collection of events 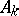forms a partition if the events are disjoint, have positive probability and if their union is the sample space.