Minimax statistical procedure
One of the versions of optimality in mathematical statistics, according to which a statistical procedure is pronounced optimal in the minimax sense if it minimizes the maximal risk. In terms of decision functions (cf. Decision function) the notion of a minimax statistical procedure is defined as follows. Let a random variable  take values in a sampling space
take values in a sampling space  ,
,  , and let
, and let  be the class of decision functions which are used to make a decision
be the class of decision functions which are used to make a decision  from the decision space
from the decision space  on the basis of a realization of
on the basis of a realization of  , that is,
, that is,  . In this connection, the loss function
. In this connection, the loss function  , defined on
, defined on  , is assumed given. In such a case a statistical procedure
, is assumed given. In such a case a statistical procedure 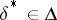 is called a minimax procedure in the problem of making a statistical decision relative to the loss function
is called a minimax procedure in the problem of making a statistical decision relative to the loss function  if for all
if for all 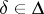 ,
,
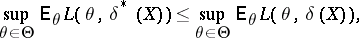 |
where
 |
is the risk function associated to the statistical procedure (decision rule)  ; the decision
; the decision 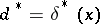 corresponding to an observation
corresponding to an observation  and the minimax procedure
and the minimax procedure  is called the minimax decision. Since the quantity
is called the minimax decision. Since the quantity
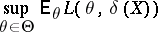 |
shows the expected loss under the procedure 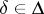 ,
,  being maximal means that if
being maximal means that if 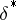 is used to choose a decision
is used to choose a decision 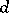 from
from 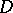 , then the largest expected risk,
, then the largest expected risk,
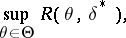 |
will be as small as possible.

Figure: m063970a
The minimax principle for a statistical procedure does not always lead to a reasonable conclusion (see Fig. a); in this case one must be guided by 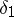 and not by
and not by  , although
, although
 |
The notion of a minimax statistical procedure is useful in problems of statistical decision making in the absence of a priori information regarding  .
.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | S. Zacks, "The theory of statistical inference" , Wiley (1971) |
Minimax statistical procedure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimax_statistical_procedure&oldid=15340