Completely distributive lattice

A complete lattice in which the identity

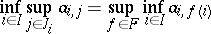(called the complete distributive law) holds for all doubly-indexed families of elements 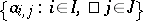, where 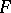is the set of all choice functions for the family of sets 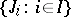. Like the finite distributive law (see Distributive lattice), the complete distributive law is equivalent to its dual; that is, a lattice 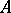is completely distributive if and only if the opposite lattice 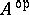is completely distributive. 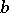Completely distributive lattices may also be characterized as those complete lattices in which every element is expressible as the supremum of elements such that, whenever 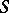is any subset of 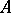with 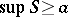, there exists an 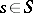with 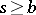[a1]. Any complete totally ordered set is completely distributive; a complete Boolean algebra is completely distributive if and only if it is isomorphic to the full power set of some set. In general, a complete lattice is completely distributive if and only if it is imbeddable in a full power set by a mapping preserving arbitrary sups and infs.

References

[a1]	G.N. Raney, "Completely distributive complete lattices" Proc. Amer. Math. Soc. , 3 (1952) pp. 677–680
[a2]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1967)