Writhing number
Let 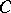 be a closed imbedded smooth curve in
be a closed imbedded smooth curve in 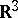 . For each ordered pair of points
. For each ordered pair of points 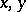 on
on 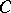 , let
, let 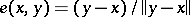 be the unit-length vector pointing from
be the unit-length vector pointing from  to
to 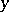 . This gives a mapping
. This gives a mapping 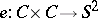 . The writhing number of the space curve
. The writhing number of the space curve 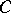 is
is
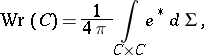 |
where 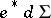 is the pull-back along
is the pull-back along  of the standard area element
of the standard area element  on the unit sphere
on the unit sphere 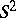 . In terms of local curve parameters
. In terms of local curve parameters 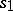 and
and 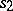 at
at  and
and 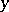 it can be described as
it can be described as
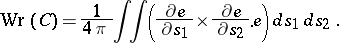 |
Now let 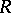 be a ribbon based on
be a ribbon based on 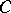 . Such a ribbon is obtained by taking a smooth vector field
. Such a ribbon is obtained by taking a smooth vector field  of unit-length vectors on
of unit-length vectors on 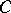 such that
such that 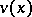 is always perpendicular to the tangent vector along
is always perpendicular to the tangent vector along 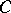 at
at 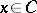 . The unit length is chosen small enough such that each unit-length line segment
. The unit length is chosen small enough such that each unit-length line segment 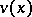 at
at  only intersects
only intersects 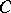 at
at  . The ribbon
. The ribbon 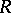 is the union of all the closed unit-length line segments
is the union of all the closed unit-length line segments 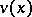 ,
, 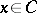 . Let
. Let 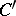 be the smooth curve of end points of the
be the smooth curve of end points of the 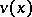 . The total twist of the ribbon
. The total twist of the ribbon 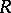 is defined as
is defined as
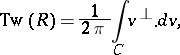 |
where 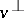 at
at 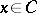 is the unit-length vector such that
is the unit-length vector such that  ,
, 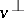 and
and 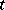 , the unit-length tangent vector along
, the unit-length tangent vector along 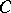 at
at  , make up a right-handed orthonormal
, make up a right-handed orthonormal  -frame. The writhing number of
-frame. The writhing number of 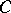 , total twist of
, total twist of 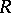 and the linking number
and the linking number 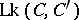 (cf. Linking coefficient), given by the Gauss formula
(cf. Linking coefficient), given by the Gauss formula
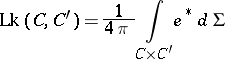 |
(where now  runs over
runs over 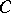 and
and 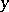 over
over 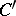 ), are related by White's formula:
), are related by White's formula:
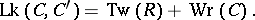 |
This formula has applications to the coiling and supercoiling of DNA.
References
| [a1] | W.F. Pohl, "DNA and differential geometry" Math. Intelligencer , 3 (1980) pp. 20–27 |
| [a2] | J.H. White, "Self-linking and the Gauss integral in higher dimensions" Amer. J. Math. , 91 (1969) pp. 693–728 |
Writhing number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Writhing_number&oldid=15244