Randomization test
permutation test
A statistical test for the hypothesis that the probability density of the random vector under observation is symmetric with respect to permutations of its arguments.
Given a realization  of a random vector
of a random vector 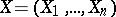 , the hypothesis
, the hypothesis 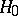 to be tested is whether or not the unknown probability density of
to be tested is whether or not the unknown probability density of 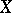 is symmetric with respect to permutations of the arguments, that is, whether
is symmetric with respect to permutations of the arguments, that is, whether
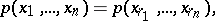 |
where 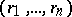 is an arbitrary permutation of
is an arbitrary permutation of 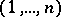 . Let
. Let 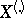 and
and 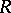 be the vector of order statistics (cf. Order statistic) and the rank vector, respectively, constructed from
be the vector of order statistics (cf. Order statistic) and the rank vector, respectively, constructed from  , and let a statistic
, and let a statistic 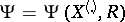 with values in
with values in 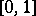 be such that for some
be such that for some 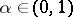 ,
,
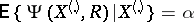 |
almost-everywhere. Then the statistical test with critical function 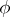 connected with
connected with  by the relation
by the relation 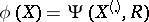 is called a randomization test. Since
is called a randomization test. Since 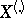 is a complete sufficient statistic, the family of similar tests (cf. Similar test) coincides with the family of permutation tests.
is a complete sufficient statistic, the family of similar tests (cf. Similar test) coincides with the family of permutation tests.
References
| [1] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Randomization test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Randomization_test&oldid=15231