Completion method

A method for calculating the inverse of a matrix, based on a recurrent transition which involves the calculation of a matrix 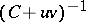, where is a column vector, is a row vector, by the formula

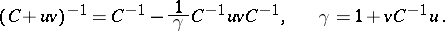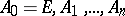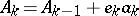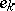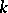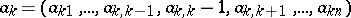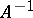The computational scheme of the method is as follows. Let be a given matrix of order . Consider a sequence , where , is the -th column of the identity matrix , . Then and the matrix is obtained by applying the above-described procedure times. The computational formulas in this case are the following: If 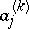is the -th column of 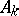, then for ,

(*)

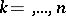It is sufficient to compute the elements of the first 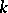rows of the matrix 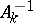, since all subsequent rows coincide with the rows of the identity matrix.

Other possibilities of arranging the computations in the completion method based on certain modifications of (*) are known, e.g. the so-called Ershov method (see [1]).

References

[1]	D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian)

Comments

This method is also called the bordering method (cf. [1]). See, however, also Bordering method.