Additive stochastic process
A real-valued stochastic process  such that for each integer
such that for each integer  and
and 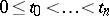 the random variables
the random variables 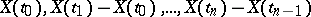 are independent. Finite-dimensional distributions of the additive stochastic process
are independent. Finite-dimensional distributions of the additive stochastic process  are defined by the distributions of
are defined by the distributions of 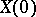 and the increments
and the increments  ,
,  .
.  is called a homogeneous additive stochastic process if, in addition, the distributions of
is called a homogeneous additive stochastic process if, in addition, the distributions of 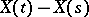 ,
, 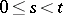 , depend only on
, depend only on 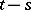 . Each additive stochastic process
. Each additive stochastic process 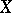 can be decomposed as a sum (see [a1])
can be decomposed as a sum (see [a1])
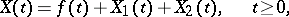 | (a1) |
where 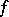 is a non-random function,
is a non-random function, 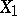 and
and 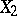 are independent additive stochastic processes,
are independent additive stochastic processes, 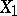 is stochastically continuous, i.e., for each
is stochastically continuous, i.e., for each  and
and 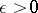 ,
, 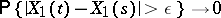 as
as  , and
, and 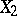 is purely discontinuous, i.e., there exist a sequence
is purely discontinuous, i.e., there exist a sequence 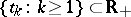 and independent sequences
and independent sequences  ,
, 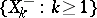 of independent random variables such that
of independent random variables such that
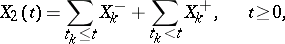 | (a2) |
and the above sums for each 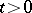 converge independently of the order of summands.
converge independently of the order of summands.
A stochastically continuous additive process 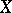 has a modification that is right continuous with left limits, and the distributions of the increments
has a modification that is right continuous with left limits, and the distributions of the increments 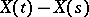 ,
, 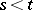 , are infinitely divisible (cf. Infinitely-divisible distribution). They are called Lévy processes. For example, the Brownian motion with drift coefficient
, are infinitely divisible (cf. Infinitely-divisible distribution). They are called Lévy processes. For example, the Brownian motion with drift coefficient 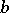 and diffusion coefficient
and diffusion coefficient 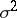 is an additive process
is an additive process 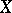 ; for it
; for it 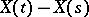 ,
, 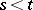 , has a normal distribution (Gaussian distribution) with mean value
, has a normal distribution (Gaussian distribution) with mean value 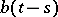 and variation
and variation 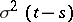 ,
, 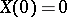 .
.
The Poisson process with parameter 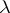 is an additive process
is an additive process 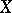 ; for it,
; for it, 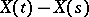 ,
,  , has the Poisson distribution with parameter
, has the Poisson distribution with parameter 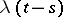 and
and 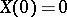 . A Lévy process
. A Lévy process 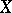 is stable (cf. Stable distribution) if
is stable (cf. Stable distribution) if 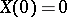 and if for each
and if for each  the distribution of
the distribution of 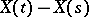 equals the distribution of
equals the distribution of 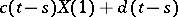 for some non-random functions
for some non-random functions  and
and 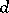 .
.
If, in (a1), (a2), 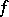 is a right-continuous function of bounded variation for each finite time interval and
is a right-continuous function of bounded variation for each finite time interval and 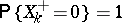 ,
, 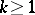 , then the additive process
, then the additive process 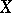 is a semi-martingale (cf. also Martingale). A semi-martingale
is a semi-martingale (cf. also Martingale). A semi-martingale 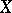 is an additive process if and only if the triplet of predictable characteristics of
is an additive process if and only if the triplet of predictable characteristics of  is non-random (see [a2]).
is non-random (see [a2]).
The method of characteristic functions (cf. Characteristic function) and the factorization identities are main tools for the investigation of properties of additive stochastic processes (see [a3]). The theory of additive stochastic processes can be extended to stochastic processes with values in a topological group. A general reference for this area is [a1].
References
| [a1] | A.V. Skorokhod, "Random processes with independent increments" , Kluwer Acad. Publ. (1991) (In Russian) |
| [a2] | B. Grigelionis, "Martingale characterization of stochastic processes with independent increments" Lietuvos Mat. Rinkinys , 17 (1977) pp. 75–86 (In Russian) |
| [a3] | N.S. Bratijchuk, D.V. Gusak, "Boundary problems for processes with independent increments" , Naukova Dumka (1990) (In Russian) |
Additive stochastic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Additive_stochastic_process&oldid=15176